Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét dấu tam thức bậc hai tức là kiểm tra về dấu của tam thức bậc hai theo từng (khoảng) giá trị của ẩn.
Ta có \(a = - 200 < 0,b = 92 000, c = 8400 000\)
\(\Delta ' = {(92000:2)}^2 - \left( { - 200} \right). 8400 000 = 436000000 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = 230 \pm 10\sqrt 109\). Khi đó:
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( { - \infty ; 230 - 10\sqrt 109} \right)\) và \(\left( {230 + 10\sqrt 109; + \infty } \right)\);
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( {230-10\sqrt 109; 230 + 10\sqrt 109} \right)\)

Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
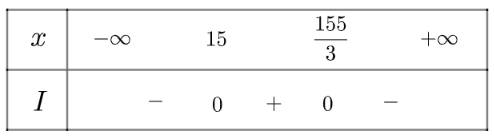
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)

Thay x vào ta có:

Dựa vào bảng trên ta thấy:
Khi x tăng, giá trị y của hàm số y=-x+1 giảm
Khi x tăng, giá trị y của hàm số y=x tăng

a) Doanh thu khi bán hết Q sản phẩm là 1200Q (nghìn đồng)
Lợi nhuận bán hết Q sản phẩm là:
\(\begin{array}{l}1200Q - \left( {{Q^2} + 180Q + 140000} \right)\\ = - {Q^2} + 1020Q - 140000\end{array}\)
b)
Để xí nghiệp hòa vốn thì: Lợi nhuận bằng 0.
\(\begin{array}{l} \Leftrightarrow - {Q^2} + 1020Q - 140000 = 0\\ \Leftrightarrow \left[ \begin{array}{l}Q \approx 857\\Q \approx 163\end{array} \right.\end{array}\)
Vậy xí nghiệp sản xuất 163 sản phẩm hoặc 857 sản phẩm thì hòa vốn.
c) Để không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0.
Khi đó:
\(\begin{array}{l} - {Q^2} + 1020Q - 140000 \ge 0\\ \Leftrightarrow 163,45 \le Q \le 857,55\\ \Rightarrow 164 \le Q \le 857\end{array}\)
Vậy để không bị lỗ thì xí nghiệp cần sản xuất số sản phẩm nằm trong khoảng 164 đến 857.

a) Tìm tập xác định của hàm số trên.
\(f\left( x \right)\) có nghĩa khi x0.
=> Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
Với \(x = - 1\), suy ta \(x < 0\)\( \Rightarrow y = - x = - \left( { - 1} \right) = 1\).
Với \(x = 2022\), suy ra \(x > 0\)\( \Rightarrow y = x = 2022\).


a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.