Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m

Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó \(DE = \frac{1}{2}BC\) suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.

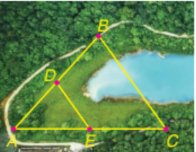
Ta có:
\(\left. \begin{array}{l}AB \bot AC\\DE \bot AC\end{array} \right\} \Rightarrow AB\parallel DE\)
Xét tam giác ABC với \(AB\parallel DE\) có:
\(\frac{{DE}}{{AB}} = \frac{{CD}}{{CA}}\) (Hệ quả của định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{18}}{{AB}} = \frac{{20}}{{50}}\\ \Rightarrow AB = 18.50:20\\ \Rightarrow AB = 45\end{array}\)
Vậy khoảng cách AB là 45m.

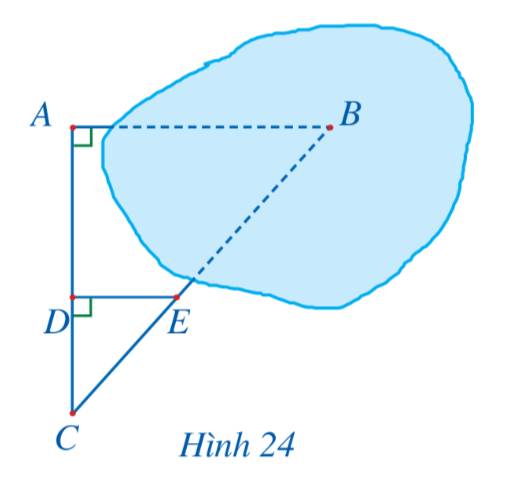
a) Cách đo:
- Chọn thêm hai điểm D và C sao cho A, D, C thẳng hàng và AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thẳng hàng và DF ⊥ AC.
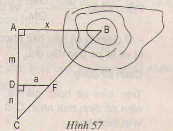
Giải:
a) Cách đo: Chọn thêm hai điểm C và D sao cho A,D,C thẳng hàng AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thằng hàng và DF ⊥ AC.
b) ∆CDF ∽ ∆CAB (DF // AB)
=> DFAB=CDCADFAB=CDCA = > AB = DF.CACD=a(m+n)mDF.CACD=a(m+n)m
vẫy x= DF.CACD=a(m+n)mDF.CACD=a(m+n)m

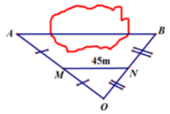
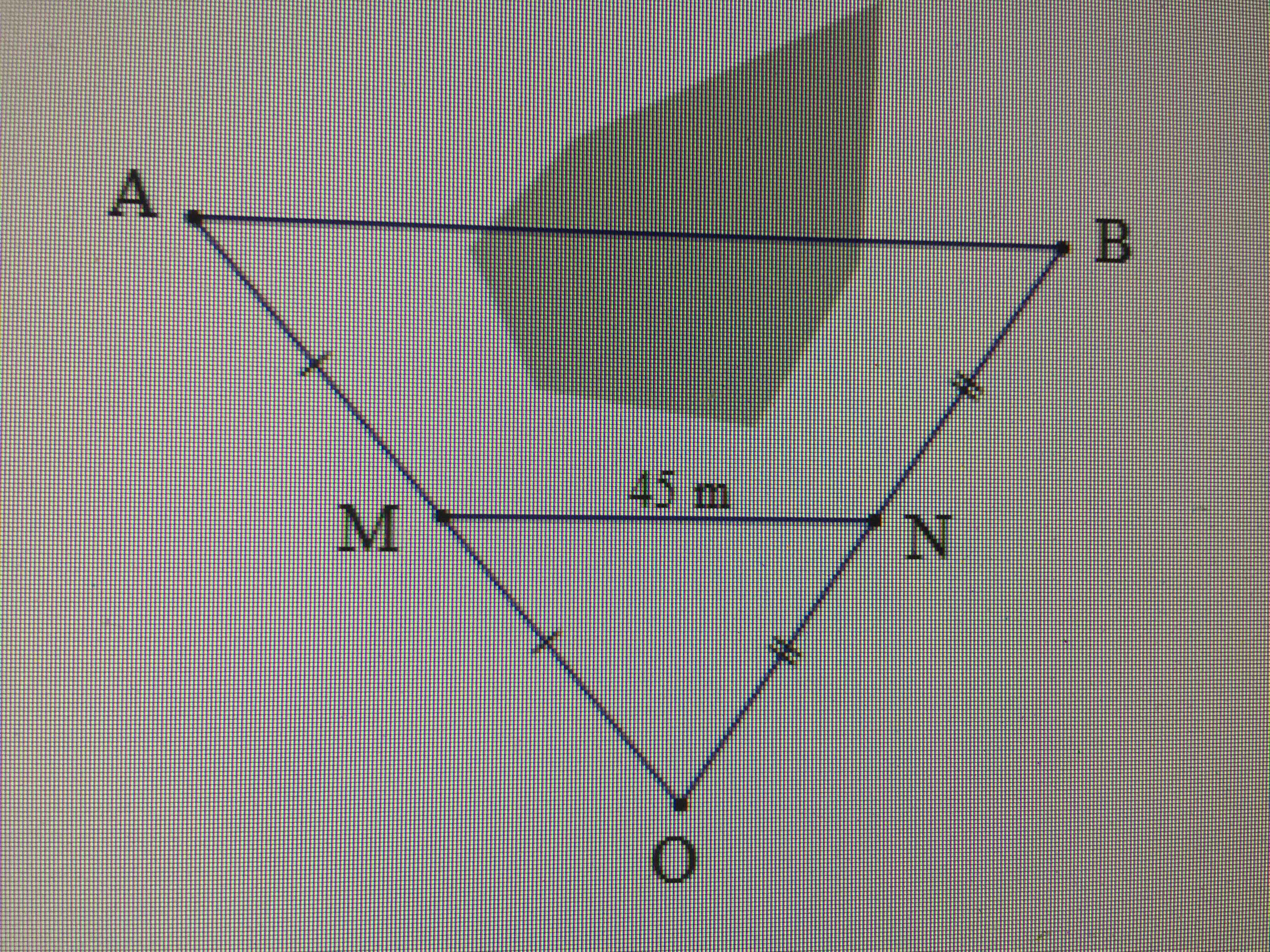
Xét tam giác OAB có:
M là trung điểm AO(gt)
N là trung điểm OB(gt)
=> MN là đường trung bình
\(\Rightarrow AB=2MN=2.45=90\left(m\right)\)

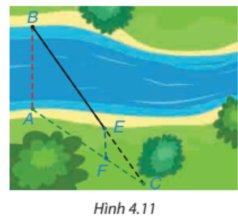
Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:
\(\dfrac{{EC}}{{BE}} = \dfrac{{CF}}{{AF}}\) hay \(\dfrac{{30}}{{BE}} = \dfrac{{20}}{{40}}\)
Suy ra \(BE = \dfrac{{30.40}}{{20}} = 60\) (m).
Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.
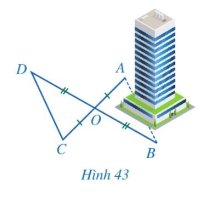



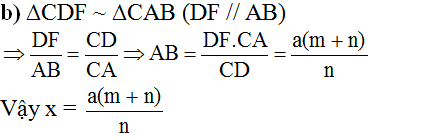
Ta có: AC giao với BD tại O.
Mà: OA = OC; OB = OD
Nên tứ giác ABCD là hình bình hành
Suy ra AB = CD = 100m.