Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

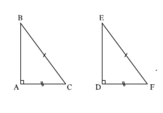
- Bổ sung AB =DE thì ΔABC = ΔDEF (c.g.c)
- Hoặc Bổ sung góc C = góc F (2 tam giác bằng nhau theo trường hợp g.c.g)
- Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền - cạnh góc vuông)

1) Số đo góc A bằng C=80
2) 3 cạnh của tam giác vuông là B
3) Kí hiệu đúng là A
4) Vậy AC=4 cm
5) a) Xét tam giác ABD và tam giác AEC có:
<AEC=<ADB=90
<BAD=<EAC (góc chung)
AB=AC (tam giác ABC cân)
Suy ra tam giác BAD=tam giác CAE (cạnh huyền- góc nhọn)
Suy ra BD=EC (vì 2 cạnh tương ứng)
b) Ta có tam giác BAD=tam giác CAE (ở câu a)
Suy ra <ADK=<AEK (vì 2 góc tương ứng)
c) Tam giác GDE ở đâu vậy bạn, bạn xem lại đề rồi mình giải cho
1) C
2) B
3) A
4) D
5) Giải.
a) Tam giác ABC cân tại A => AB = AC
Góc B = góc C
Xét 2 tam giác vuông, EBC và DCB, có:
Góc B = góc C (cmt)
Cạnh BC chung
=> Tam giác EBC = tam giác DCB.
=> BD = CE ( 2 cạnh tương ứng)
Đề câu b,c hơi sai sai bn viết lại đc hk

bạn tự vẽ hình nha
áp dụng địng lí py ta go vào tam giác ABC vuông ở A
=> \(BC^2=AB^2+AC^2\)
=\(6^2+8^2\)
=36+64
=100
=> BC=10cm
a) ta có định lí: trong 1 tam giác vuông đường trung tuyến ứng với cạnh huyền thì = nửa cạnh huyền
=> AM=\(\frac{BC}{2}\)=\(\frac{10}{2}\)=5 cm
b)xét 2 tam giác AMB và DMC có:
AM =MD(gt)
BM=CM(AM là trung tuyến)
góc AMB=góc DMC(đối đỉnh)
=> 2 tam giác AMB=DMC(c.g.c)
c)
cì AM =\(\frac{BC}{2}=BM=CM\)
mà AM =DM(gt)
=> AM+DM=BM+CM hay AD=BC
2 tam giác ABM=DMC(theo b)
=> AB=DC(2 cạnh tương ứng)
xét 2 tam giác ABC và CDA có:
AB =DC(chứng minh trên )
AD =BC(chứng minh trên)
cạnh AC chung
=> 2 tam giác ABC =CDA(c.c.c)
=> 2góc BAC=DCA=90độ(2 góc tương ứng)
hay AC vuông góc với DC

a, Xét △ABM vuông tại A và △DBM vuông tại D
Có: BM là cạnh chung
∠ABM = ∠DBM (gt)
=> △ABM = △DBM (ch-gn)
b, Xét △ABC vuông tại A và △DBE vuông tại D
Có: AB = DB (△ABM = △DBM)
∠ABC là góc chung
=> △ABC = △DBE (cgv-gnk)
=> AC = DE (2 cạnh tương ứng)
c, Xét △AME vuông tại A và △DMC vuông tại D
Có: AM = MD (△ABM = △DBM)
∠AME = ∠DMC (2 góc đối đỉnh)
=> △AME = △DMC (cgv-gnk)
d, Vì AB = BD (cmt) => B thuộc đường trung trực của AD
Vì AM = DM (cmt) => M thuộc đường trung trực của AD
=> BM là đường trung trực của AD
=> BM ⊥ AD
e, Xét △DHC vuông tại K và △AKE vuông tại H
Có: DC = AE (△DMC = △AME)
∠DCH = ∠AEK (△ABC = △DBE)
=> △DHC = AKE (ch-gn)
f, Xét △AMK vuông tại K và △DMH vuông tại H
Có: AM = MD (cmt)
∠AMK = ∠DMH (2 góc đối đỉnh)
=> △AMK = △DMH (ch-gn)
=> MK = MH (2 cạnh tương ứng)
Xét △MKN vuông tại K và △MHN vuông tại H
Có: MK = MH (cmt)
MN là cạnh chung
=> △MKN = △MHN (ch-cgv)
=> ∠KMN = ∠HMN (2 góc tương ứng)
=> MN là phân giác KMH
g, Ta có: AK + KN = AN và DH + HN = DN
Mà AK = DH (△AMK = △DMH) ; KN = HN (△MKN = △MHN)
=> AN = DN
Xét △BAN và △BDN
Có: AB = BD (cmt)
AN = DN (cmt)
BN là cạnh chung
=> △BAN = △BDN (c.c.c)
=> ∠ABN = ∠DBN (2 góc tương ứng)
=> BN là phân giác ABD
Mà BM là phân giác ABD
=> BN ≡ BM
=> 3 điểm B, M, N thẳng hàng
h, Để △ADN là tam giác đều mà AN = DN (cmt)
<=> ∠AND = 60o <=> ∠ANM + ∠MND = 60o
Mà ∠ANM = ∠MND (△BAN = △BDN)
<=> ∠ANM = ∠MND = 30o
Vì AB ⊥ AC (gt) và DH ⊥ AC (gt) => DN ⊥ AC
=> AB // DN
=> ∠ABN = ∠BND (2 góc so le trong) và ∠ANB = ∠NBD (2 góc so le trong)
Mà ∠ANB = ∠BND = 30o (cmt)
=> ∠ABN = ∠NBD = 30o
=> ∠ABN + ∠NBD = 30o + 30o
=> ∠ABD = 60o
=> ∠ABC = 60o
Vậy để △ADN là tam giác đều khi △ABC có ∠ABC = 60o


Chọn A
D