
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Đáp án D
Gọi z = x + y i , x , y ∈ ℝ .
Ta có x 2 + y − 1 2 = 16, x = 0 ⇒ y = − 3 y = 5 .
Vậy có 2 số phức thỏa mãn đề bài

Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .


Theo hệ quả của bất đẳng thức Cauchy - Schwarz
\(\Rightarrow x^2+y^2+z^2\ge xy+yz+xz\)
Mà \(x^2+y^2+z^2\le3\)
\(\Rightarrow xy+yz+xz\le3\)
Ta có \(P=\dfrac{1}{1+xy}+\dfrac{1}{1+yz}+\dfrac{1}{1+xz}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow P\ge\dfrac{\left(1+1+1\right)^2}{xy+1+yz+1+xz+1}=\dfrac{9}{xy+yz+xz+3}\) (1)
Ta có \(xy+yz+xz\le3\)
\(\Rightarrow xy+yz+xz+3\le6\)
\(\Rightarrow\dfrac{9}{xy+yz+xz+3}\ge\dfrac{9}{6}=\dfrac{3}{2}\) (2)
Từ (1) và (2)
\(\Rightarrow P\ge\dfrac{3}{2}\)
Vậy \(P_{min}=\dfrac{3}{2}\)
Dấu " = " xảy ra khi \(x=y=z=1\)

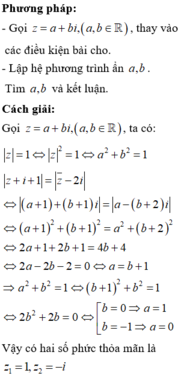




Chọn đáp án B
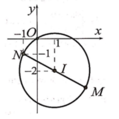
Giả sử tồn tại số phức z = x + y i x , y ∈ ℝ thỏa mãn yêu cầu bài toán
Từ giả thiết ta có hệ
Do phương trình * vô nghiệm nên hệ trên vô nghiệm. Vậy không tồn tại số phức nào thỏa mãn yêu cầu bài toán