Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
- Đặt sinx = t, biến đổi điều kiện bài cho về điều kiện của phương trình ẩn t.
- Sử dụng bảng biến thiên để tìm điều kiện của m.
Cách giải:
![]()
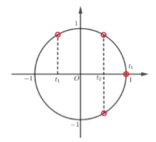
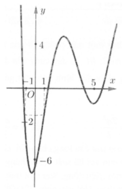
Phương trình đã cho có đúng 3 nghiệm phân biệt thuộc khoảng − π 2 ; π




![]()
![]()
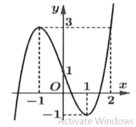
Do đó phương trình f[f(sinx)] = m có nghiệm thuộc khoảng 0 ; π khi và chỉ khi phương trình
f(t) = m có nghiệm thuộc nửa khoảng [-1;1]
Dựa vào đồ thị, suy ra ![]()
Chọn C.

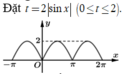
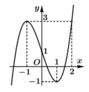
Dựa vào đồ thị y= 2|sinx| trên
-
π
;
2
π
, ta thấy t = 0 cho ta 4 nghiệm ![]()

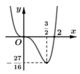
Dựa vào đồ thị hàm số
y
=
f
x
ta thấy phương trình ![]() có tối đa 2 nghiệm (đường thẳng y =
f
m
2
cắt đồ thị tối đa hai điểm).
có tối đa 2 nghiệm (đường thẳng y =
f
m
2
cắt đồ thị tối đa hai điểm).
Do đó để phương trình đã cho có đúng 12 nghiệm x phân biệt thuộc
-
π
;
2
π
khi và chỉ khi phương trình ![]() có đúng 2 nghiệm t phân biệt thuộc (0;2)
có đúng 2 nghiệm t phân biệt thuộc (0;2)
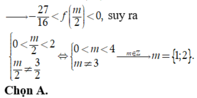
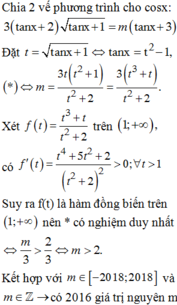







Đáp án B