Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn 2 trong 5 giáo viên có: C 5 2 = 10 cách chọn.
Chọn 3 trong 6 học sinh có C 6 3 = 20 cách chọn.
Vậy có 10. 20 = 200 cách chọn.
Chọn đáp án A

a.
Số cách chọn: \(A_6^3=120\) cách
b.
Số cách chọn: \(C_4^2.C_2^1=12\) cách

a. Có \(C_6^3\) cách chọn 3 nam từ 6 nam
b.
Chọn 2 nam từ 6 nam và 3 nữ từ 9 nữ để lập tổ 1 có: \(C_6^2.C_9^3\) cách
Chọn 2 nam từ 4 nam còn lại và 3 nữ từ 6 nữ còn lại để lập tổ 2 có: \(C_4^2.C_6^3\) cách
Chọn 2 nam từ 2 nan còn lại và 3 nữ từ 3 nữ còn lại: \(C_2^2.C_3^3\) cách
\(\Rightarrow C_6^2.C_9^3+C_4^2.C_6^3+C_2^2.C_3^3\) cách thỏa mãn chia 3 tổ

TH 1: 4 học sinh được chọn thuộc một lớp:
A: có cách chọn C 5 4 = 5
B: có cách chọn C 4 4 = 1
Trường hợp này có: 6 cách chọn.
TH 2: 4 học sinh được chọn thuộc hai lớp:
A và B: có C 9 4 - ( C 5 4 + C 4 4 ) = 120
B và C: có C 9 4 - C 4 4 = 125
C và A: có C 9 4 - C 5 4 = 121
Trường hợp này có 366 cách chọn.
Vậy có 366+6=372 cách chọn thỏa yêu cầu bài toán.
Chọn C.

Đáp án B
n ( Ω ) = C 12 4
Gọi H:” Không có quá 2 trong 3 lớp”
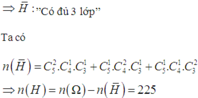

a.
Chọn 4 bạn bất kì từ 3 lớp: \(C_{12}^4\)
Chọn 4 bạn ko có lớp A: \(C_9^4\)
Chọn 4 bạn ko có lớp B: \(C_8^4\)
Chọn 4 bạn ko có lớp C: \(C_7^4\)
Số cách thỏa mãn: \(C_{12}^4-\left(C_7^4+C_8^4+C_9^4\right)=...\)
b.
Chọn 4 bạn có đúng 1 bạn lớp A: \(C_3^1.C_9^3\)
Số các thỏa mãn:
\(C_{12}^4-\left(3.C_9^3+C_9^4\right)\)

Gọi A là tập hợp mọi cách chọn 4 học sinh trong 12 học sinh
Gọi B là tập hợp cách chọn không thỏa mãn yêu cầu đề bài (tức là chọn đủ học sinh 3 lớp)
Gọi C là tập hợp cách chọn thỏa mãn yêu cầu đề bài
Ta có A = B\(\cup\) C, B \(\cap\) C = \(\varnothing\)
Theo quy tắc cộng ta có
\(\left|A\right|\) = \(\left|B\right|\) + \(\left|C\right|\) \(\Rightarrow\) \(\left|C\right|\) = \(\left|A\right|\) - \(\left|B\right|\) (1)
Dễ thấy \(\left|A\right|\) = \(C_{12}^4\) = 495
Để tính \(\left|B\right|\), ta nhận thấy sẽ chọn một lớp có 2 học sinh, còn 2 lớp còn lại mỗi lớp 1 học sinh. Vì thế theo quy tắc cộng và phép nhân, ta có:
\(\left|B\right|\) = \(C_5^2\)\(C_4^1\)\(C_3^1\) + \(C_5^1\)\(C_4^2\)\(C_3^1\) + \(C_5^1\)\(C_4^1\)\(C_3^2\) = 120 + 90 + 60 = 270
Thay vào (1) ta có \(\left|C\right|\) = 495 - 270 = 225
Vậy có 225 cách chọn.
Số cách chọn 4 học sinh từ 12 học sinh đã cho là : C412=495C124=495
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau :
* Lớp AA có 2 học sinh, các lớp BB, CC mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C25.C14.C13=120C52.C41.C31=120
* Lớp BB có 2 học sinh, các lớp AA, CC mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C15.C24.C13=90C51.C42.C31=90
Lớp CC có 2 học sinh, các lớp AA, BB mỗi lớp 1 học sinh.
⇒⇒ Số cách chọn là : C15.C14.C23=60C51.C41.C32=60
Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là :
120+90+60=270120+90+60=270
Vậy số cách chọn phải tìm là : 495−270=225495−270=225 cách.

Chọn D
Số cách chọn hai học sinh từ một nhóm gồm 41 học sinh là số tổ hợp chập 2 của 41, tức có C 41 2 cách chọn.