CMR 2013x+m(sin2x−cos2x)=2014Π có nghiệm với mọi m

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

LT

lê trung

14 tháng 2 2019

CMR 2013x+m(sin2x−cos2x)=2014Π có nghiệm với mọi m

#Hỏi cộng đồng OLM #Toán lớp 11

1

TV

Truong Viet Truong

8 tháng 3 2019

Hỏi đáp Toán

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

13 tháng 6 2019

Tìm tất cả giá trị của m để phương trình sin²x – 2( m- 1)sinx. cosx – (m- 1).cos²x = m có nghiệm?

A. 0 ≤ m ≤ 1

B.m> 1

C.0< m< 1

D. m ≤ 0

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

13 tháng 6 2019

Hướng dẫn giải:

Chọn A.

Ta có: sin²x – 2( m- 1)sinx. cosx – (m- 1).cos²x = m

PT

Pham Trong Bach

21 tháng 6 2017

Tìm m để các bất phương trình 4 sin 2 x + cos 2 x + 17 3 cos 2 x + sin 2 x + m + ...

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

21 tháng 6 2017

Đáp án B

PT

Pham Trong Bach

18 tháng 7 2017

Tìm m để các bất phương trình sau đúng với mọi x 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x ...

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

18 tháng 7 2017

Đáp án D

DQ

Đặng Quang Vinh

28 tháng 10 2021

cho pt; 1-sin2x+cos2x-2mcosx=0

tìm m để pt có 2 nghiệm thuộc (-π;π)

#Hỏi cộng đồng OLM #Toán lớp 11

0

NM

Nguyễn Mai Chi

11 tháng 4 2020

Tìm đạo hàm của các hàm số sau:

a)y= sin2x+cos2x / 2sin2x-cos2x

b)y=4sinx.cos5x.sin6x

c)y= sin2x+cos2x / sin2x-cos2x

#Hỏi cộng đồng OLM #Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

11 tháng 4 2020

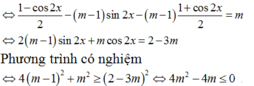
a/ \(y'=\frac{\left(2cos2x-2sin2x\right)\left(2sin2x-cos2x\right)-\left(sin2x+cos2x\right)\left(4cos2x+2sin2x\right)}{\left(2sin2x-cos2x\right)^2}\)

\(=\frac{3sin4x-2cos^22x-4sin^22x-3sin4x-2sin^22x-4cos^22x}{\left(2sin2x-cos2x\right)^2}\)

\(=\frac{-6cos^22x-6sin^22x}{\left(2sin2x-cos2x\right)^2}=-\frac{6}{\left(2sin2x-cos2x\right)^2}\)

b/ \(y'=4cosx.cos5x.sin6x+4sinx\left(cos5x.sin6x\right)'\)

\(=4cosx.cos5x.sin6x+4sinx\left(-5sin5x.sin6x+6cos5x.cos6x\right)\)

\(=4cosx.cos5x.sin6x+4sinx\left(6cos11x+sin5x.sin6x\right)\)

\(=4sin6x\left(cosx.cos5x+sinx.sinx\right)+24sinx.cos11x\)

\(=4sin6x.cos4x+24sinx.cos11x\)

c/ \(y'=\frac{\left(2cos2x-2sin2x\right)\left(sin2x-cos2x\right)-\left(sin2x-cos2x\right)\left(2cos2x+2sin2x\right)}{\left(sin2x-cos2x\right)^2}\)

\(=\frac{-2\left(sin2x-cos2x\right)^2-2\left(sin2x-cos2x\right)\left(sin2x+cos2x\right)}{\left(sin2x-cos2x\right)^2}\)

\(=\frac{-2\left(sin2x-cos2x\right)-2\left(sin2x+cos2x\right)}{sin2x-cos2x}=\frac{-4sin2x}{sin2x-cos2x}\)

AP

Annh Phươngg

5 tháng 4 2022

cho hàm số f(x)=sin2x+2(1-2m)cos2x-2mx+1. Với giá trị nào của tham số m thì phương trình f'(x)=0 có nghiệm

#Hỏi cộng đồng OLM #Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

5 tháng 4 2022

\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)

Phương trình \(f'\left(x\right)=0\) có nghiệm

\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm

\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(1^2+4\left(1-2m\right)^2\ge m^2\)

\(\Leftrightarrow15m^2-16m+5\ge0\)

\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)

Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m

PT

Pham Trong Bach

19 tháng 1 2017

Tìm m để hàm số y = 2 sin 2 x + 4 sinx cosx - ( 3 + 2 m ) cos 2 ...

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

19 tháng 1 2017

Đáp án D

Hàm số xác định với mọi x

⇔ 2sin²x + 4sinx cosx – (3 + 2m)cos²x + 2 ≤ 0 ∀x ∈ R (1)

cos x = 0 => (1) đúng

cos x ≠ 0 khi đó ta có: (1) ⇔ 2tan²x + 4tanx – (3 + 2m) + 2(1 + tan²x) ≥ 0

⇔ 4tan²x + 4tanx ≥ 1 + 2m ∀x ∈ R

⇔ (2tanx + 1)² ≥ 2 + 2m ∀x ∈ R ⇔ 2 + 2m ≤ 0 ⇔ m ≤ -1

PT

Pham Trong Bach

28 tháng 5 2019

Tìm tất cả các giá trị của m để bất phương trình 3 . sin 2 x + cos 2 x sin 2 x + ...

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

28 tháng 5 2019

BC

Big City Boy

9 tháng 9 2023

Tìm m để phương trình sau có nghiệm:

\(4sin\left(x+\dfrac{\pi}{3}\right).cos\left(x-\dfrac{\pi}{6}\right)=m^2+\sqrt{3}.sin2x-cos2x\)

#Hỏi cộng đồng OLM #Toán lớp 11

1

ND

Nguyễn Đức Trí

9 tháng 9 2023

\(4sin\left(x+\dfrac{\pi}{3}\right).cos\left(x-\dfrac{\pi}{6}\right)=m^2+\sqrt[]{3}sin2x-cos2x\)

\(\Leftrightarrow4.\left(-\dfrac{1}{2}\right)\left[sin\left(x+\dfrac{\pi}{3}+x-\dfrac{\pi}{6}\right)+sin\left(x+\dfrac{\pi}{3}-x+\dfrac{\pi}{6}\right)\right]=m^2+2.\left[\dfrac{\sqrt[]{3}}{2}.sin2x-\dfrac{1}{2}.cos2x\right]\)

\(\Leftrightarrow2\left[sin\left(2x+\dfrac{\pi}{6}\right)+sin\left(2x-\dfrac{\pi}{6}\right)\right]=m^2+2\)

\(\Leftrightarrow2.2sin2x.cos\dfrac{\pi}{6}=m^2+2\)

\(\Leftrightarrow2.2sin2x.\dfrac{\sqrt[]{3}}{2}=m^2+2\)

\(\Leftrightarrow2\sqrt[]{3}sin2x.=m^2+2\)

\(\Leftrightarrow sin2x.=\dfrac{m^2+2}{2\sqrt[]{3}}\)

Phương trình có nghiệm khi và chỉ khi

\(\left|\dfrac{m^2+2}{2\sqrt[]{3}}\right|\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m^2+2}{2\sqrt[]{3}}\ge-1\\\dfrac{m^2+2}{2\sqrt[]{3}}\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2\ge-2\left(1+\sqrt[]{3}\right)\left(luôn.đúng\right)\\m^2\le2\left(1-\sqrt[]{3}\right)\end{matrix}\right.\)

\(\Leftrightarrow-\sqrt[]{2\left(1-\sqrt[]{3}\right)}\le m\le\sqrt[]{2\left(1-\sqrt[]{3}\right)}\)