Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
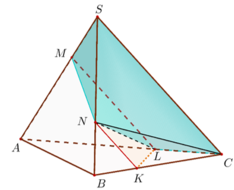
Chia khối đa diện SCMNKL bởi mặt phẳng (NLC) được hai khối chóp N. SMLC và N. LKC. Vì SC song song với (MNKL) nên SC // ML //NK
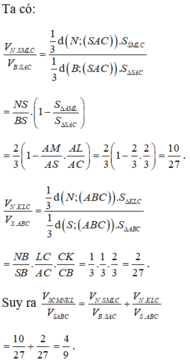

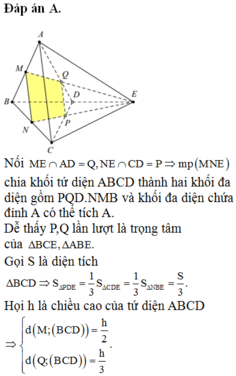
A B D M N P Q E C
Kẻ \(MP\) và \(NQ\) lần lượt song song AC \(\Rightarrow MNQP\) là thiết diện
Kéo dài \(BD;MN;PQ\) đồng quy tại E (theo tính chất giao tuyến 3 mặt phẳng)
Áp dụng định lý Talet ta có \(DQ=\frac{1}{3}CD\) ; \(BP=\frac{2}{3}BC\)
\(\Rightarrow PB=2PC\) ; \(QC=2QD\)
Áp dụng định lý Menelaus cho tam giác \(BCD\) với 3 điểm thẳng hàng P; Q; E ta có:
\(\frac{PB}{PC}.\frac{QC}{QD}.\frac{ED}{EB}=1\) \(\Leftrightarrow\frac{2}{1}.\frac{2}{1}.\frac{ED}{EB}=1\Rightarrow ED=\frac{1}{4}EB\Rightarrow DB=3ED\)
\(\Rightarrow d\left(E;CD\right)=\frac{1}{3}d\left(B;CD\right)\)
\(\Rightarrow S_{\Delta EDQ}=\frac{1}{2}DQ.d\left(E;CD\right)=\frac{1}{2}.\frac{1}{3}CD.\frac{1}{3}d\left(B;CD\right)=\frac{1}{9}S_{\Delta BCD}\)
\(S_{BDQP}=S_{BCD}-S_{CPQ}=S_{BCD}-\frac{1}{2}.CP.d\left(Q;BC\right)\)
\(=S_{BCD}-\frac{1}{2}.\frac{1}{3}BC.\frac{2}{3}d\left(D;BC\right)=S_{BCD}-\frac{2}{9}S_{BCD}=\frac{7}{9}S_{BCD}\)
\(\Rightarrow S_{EBP}=\frac{8}{9}S_{BCD}\)
\(\Rightarrow V_{M.EBP}=\frac{1}{3}S_{EBP}.d\left(M;\left(BCD\right)\right)=\frac{1}{3}.\frac{8}{9}S_{BCD}.\frac{2}{3}d\left(A;BCD\right)=\frac{16}{27}V_{A.BCD}\)
\(V_{N.EDQ}=\frac{1}{3}S_{EDQ}.d\left(N;\left(BCD\right)\right)=\frac{1}{3}.\frac{1}{9}S_{BCD}.\frac{1}{3}d\left(A;\left(BCD\right)\right)=\frac{1}{27}V_{A.BCD}\)
\(\Rightarrow V_1=V_{BMP.DNQ}=\left(\frac{16}{27}-\frac{1}{27}\right)V_{A.BCD}=\frac{15}{27}V_{ABCD}\)
\(\Rightarrow V_2=V_{ABCD}-V_1=\frac{12}{27}V_{ABCD}\)
\(\Rightarrow\frac{V_1}{V_2}=\frac{15}{12}=\frac{5}{4}\)
// Dài quá, chắc chắn đây ko phải là cách tối ưu :(

Đáp án B
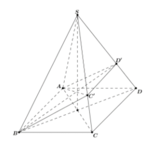
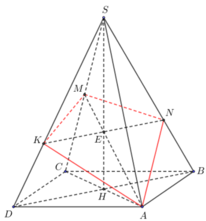
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.

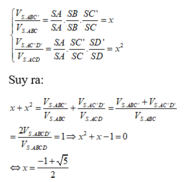
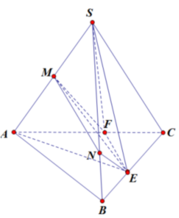


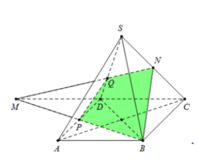

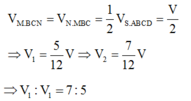
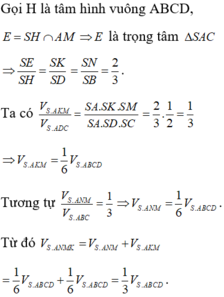
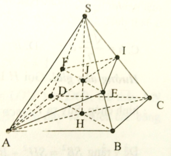
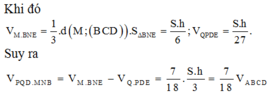
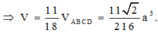
Ý bạn "tứ giác" là "tứ diện"?
Ta có: \(V_{S.ABC}=\frac{1}{3}d\left(S;\left(ABC\right)\right).S_{\Delta ABC}\)
Mặt phẳng \(\left(\alpha\right)\) hay mặt phẳng (MAB) chia tứ diện thành 2 khối tứ diện: SABM và MABC
Ta có: \(V_{M.ABC}=\frac{1}{3}d\left(M;\left(ABC\right)\right).S_{\Delta ABC}\)
Mà \(MC=\frac{1}{2}SC\Rightarrow d\left(M;\left(ABC\right)\right)=\frac{1}{2}d\left(S;\left(ABC\right)\right)\)
\(\Rightarrow V_{MABC}=\frac{1}{3}.\frac{1}{2}d\left(S;\left(ABC\right)\right).S_{\Delta ABC}=\frac{1}{2}V_{SABC}\)
\(\Rightarrow\) Hai phần có thể tích bằng nhau
Tỉ số thể tích bằng 1