

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.

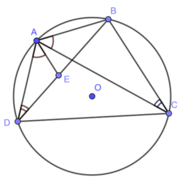
Tổng quát cho câu 2 là định lí Ptolemy, như sau: Cho \(ABCD\) nội tiếp bất kì. Khi đó \(AC.BD=AB.CD+AD.BC\).
A B C D E
CM: Vẽ \(E\in AC\) sao cho \(\widehat{ABD}=\widehat{EBC}\).
Khi đó có hai tam giác sau đồng dạng \(ABD\) và \(EBC\), \(ABE\) và \(DBC\).
Suy ra tỉ lệ cạnh: \(\frac{AD}{EC}=\frac{BD}{BC}\) và \(\frac{AB}{DB}=\frac{AE}{DC}\).
Hay \(AD.BC=BD.EC\) và \(AB.DC=AE.DB\)
Cộng lại: \(AB.CD+AD.BC=BD\left(AE+EC\right)=AC.BD\)

vì tứ giác ABCD nội tiếp,theo định lý Ptoleme ta có:
AC.BD=AB.CD+AD.BC (ĐPCM)
