Question

[dude random]

Cho tam giác OAB vuông tại A, kẻ tia OC là tia phân giác của AOB, lấy điểm H trên tia OB sao cho OA = OH a) Chứng minh tam giác OAC = OHC b) Chứng minh CH vuông góc với OB c) Tia HC cắt tia OA tại M. Chứng minh tam giác OMB là tam giác cân d) Kẻ CK vuông góc MB (K thuộc MB). Chứng minh O,C,K thẳng hàng

Answer 1

[Nguyễn Lê Phước Thịnh]

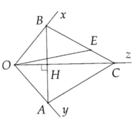
a: Xét ΔOAC và ΔOHC có

OA=OH

\(\widehat{AOC}=\widehat{HOC}\)

OC chung

Do đó: ΔOAC=ΔOHC

b: ΔOAC=ΔOHC

=>\(\widehat{OAC}=\widehat{OHC}\)

=>\(\widehat{OHC}=90^0\)

=>CH\(\perp\)OB

c: Xét ΔOHM vuông tại H và ΔOAB vuông tại A có

OH=OA

\(\widehat{HOM}\) chung

Do đó: ΔOHM=ΔOAB

=>OM=OB

=>ΔOMB cân tại O

d: Xét ΔOMB có

MH,BA là các đường cao

MH cắt BA tại C

Do đó:C là trực tâm của ΔOMB

=>OC\(\perp\)MB

mà CK\(\perp\)MB

và OC,CK có điểm chung là C

nên O,C,K thẳng hàng

Answer 2

[lai minh quan]

Để giải bài toán này, ta sẽ làm từng phần một theo các yêu cầu đã cho.

a) Chứng minh tam giác OAC = OHC

Giải:

• Ta có:
• • OA = OH (theo đề bài).
  • Chi tiết H từ OB nên OH = OA.
  • Tia OC là tia phân giác của AOB, suy ra ∠AOC = ∠HOB.

Vì vậy, hai tam giác OAC và OHC có:

• OA = OH (cạnh)
• ∠AOC = ∠HOB (góc)
• OC chung

Áp dụng tiêu chí cạnh-góc-cạnh (CGC), ta có:

\(\triangle O A C \cong \triangle O H C\)

b) Chứng minh CH vuông góc với OB

Giải:
Vì OC là tia phân giác của góc AOB, có nghĩa là:

• ∠AOC = ∠HOB.

Ta sẽ chứng minh rằng CH vuông góc với OB:

• Trong hai tam giác OAC và OHC, ta đã chứng minh OAC = OHC.
• Do đó, các góc còn lại của các tam giác bằng nhau:
• • ∠OAC = ∠OHC.

Bây giờ, ta chứng minh CH vuông góc với OB:

• Từ tính chất của phân giác, có: ∠AOB = ∠HOC.
• Vì ∠AOB = ∠AOC + ∠HOC, ta suy ra rằng ∠HOC = ∠AOB - ∠AOC.

Từ đây, ta có thể kết luận:

\(\angle O H C + \angle A O B = 9 0^{\circ} ,\)

suy ra CH vuông góc với OB.

c) Chứng minh tam giác OMB là tam giác cân

Giải:
Tia HC cắt OA tại M:

• Ta cần chứng minh OB = OM.

Ta đã chứng minh rằng:

• OA = OH và CH vuông góc với OB.

Vì H trên OB và từ H đến A đo bằng OA:

• OM = OA.

Vì OA = OH, và tam giác OAC và OHC là đồng dạng, ta có:

• OB = OM.

Do đó, ta có:

\(O A = O M \Rightarrow \triangle O M B \&\text{nbsp};\text{l} \overset{ˋ}{\text{a}} \&\text{nbsp};\text{tam}\&\text{nbsp};\text{gi} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{c} \hat{\text{a}} \text{n}.\)

d) Kẻ CK vuông góc MB (K thuộc MB). Chứng minh O, C, K thẳng hàng

Giải:
Kẻ CK vuông góc với MB tại K:

• Ta chứng minh O, C, K thẳng hàng.

Với CK vuông góc MB, ta có:

• MB là phương của những điểm M, B có cùng khoảng cách từ O đến K.
• Theo lý thuyết tam giác đồng dạng, tại góc C, K nằm trên đường thẳng đi qua O và C.
• Do đó, sẽ có điểm K thỏa mãn:
• • CK ⊥ MB,
  • và cả O, C, K đều thẳng hàng.

Suy ra:

• O, C, K thẳng hàng.

Kết luận:

Chúng ta đã chứng minh được rằng tam giác OAC = OHC, CH vuông góc với OB, OMB là tam giác cân và O, C, K thẳng hàng như yêu cầu của bài toán.