Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

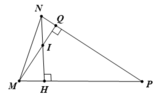
b. Với ∠(MPQ) = 60o, ∠(NMP) = 60o thì tam giác MNP cân tại N và có 1 góc bẳng 60o nên tam giác ABC là tam giác đều ( 1 điểm)
Suy ra AB = BC = AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)
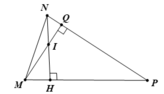
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)

a. Hình vẽ ( 1 điểm)
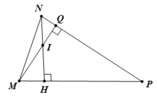
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)

Đặt:
\(\angle N M P = A , \angle M N P = B , \angle M P N = C .\)
Khi đó:
\(A + B + C = 180^{\circ} .\)
- Vì \(I\) nằm trên phân giác của \(\angle N\) nên:
\(\angle M N I = \frac{B}{2} .\)
- Vì \(I\) nằm trên phân giác của \(\angle P\) nên:
\(\angle M P I = \frac{C}{2} .\)
Xét tứ giác \(M - N - I - P\), ta có:
\(\angle M N I + \angle N I P + \angle M P I + \angle N M P = 360^{\circ} .\)
Thay các giá trị:
\(\frac{B}{2} + \angle N I P + \frac{C}{2} + A = 360^{\circ} .\)
Suy ra:
\(\angle N I P = 360^{\circ} - \left(\right. A + \frac{B}{2} + \frac{C}{2} \left.\right) .\)
Mà (A + B + C = 180^\circ \implies \dfrac{B}{2} + \dfrac{C}{2} = 90^\circ - \dfrac{A}{2}.
]
Thay vào:
\(\angle N I P = 360^{\circ} - \left(\right. A + 90^{\circ} - \frac{A}{2} \left.\right) = 360^{\circ} - \left(\right. 90^{\circ} + \frac{A}{2} \left.\right) = 270^{\circ} - \frac{A}{2} .\)
Do góc \(\angle N I P\) là góc trong (< 180°), ta có:
\(\angle N I P = 90^{\circ} + \frac{A}{2} .\)
đáp số:...
Xét ΔMNP có \(\hat{MNP}+\hat{MPN}+\hat{NMP}=180^0\)
=>\(\hat{MNP}+\hat{MPN}=180^0-\hat{PMN}\)
=>\(2\left(\hat{INP}+\hat{IPN}\right)=180^0-\hat{NMP}\)
=>\(\hat{INP}+\hat{IPN}=90^0-\hat{NMP}\cdot\frac12\)
Xét ΔNIP có \(\hat{INP}+\hat{IPN}+\hat{PIN}=180^0\)
=>\(\hat{PIN}=180^0-\left(90^0-\hat{NMP}\cdot\frac12\right)=90^0+\hat{NMP}\cdot\frac12\)
b. Với ∠(MPQ) = 60o, ∠(NMP) = 60o thì tam giác MNP cân tại N và có 1 góc bẳng 60o nên tam giác ABC là tam giác đều ( 1 điểm)
Suy ra AB = BC = AC ( 1 điểm)