

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



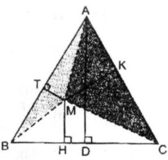
Giả sử ΔABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.
Ta có:
S A B C = 1/2 ah
S M A B = 1/2 MT.a
S M A C = 1/2 MK.a
S M B C = 1/2 MH.a
S A B C = S M A B + S M A C + S M B C
1/2 a.h = 1/2 MT.a + 1/2 MK.a + 1/2 MH.a
1/2 a. (MT + MK + MH)
⇒ MT + MK + MH = h không đổi
Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.

Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC
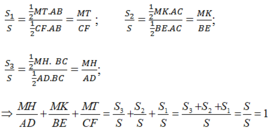

A B C D E F H K M I G
a) Ta có:
\(\left\{{}\begin{matrix}BH\perp AC\\KC\perp AC\end{matrix}\right.\) ⇒ \(BH\text{//}KC\)
\(\left\{{}\begin{matrix}CH\perp AB\\BK\perp AB\end{matrix}\right.\) ⇒ \(CH\text{//}BK\)
\(Xét\) \(tứ\) \(giác\) \(BKCH\) \(có:\) \(\left\{{}\begin{matrix}BH\text{//}KC\\CH\text{//}BK\end{matrix}\right.\)
⇒ Tứ giác \(BKCH\) là hình hình hành. Mà M là trung điểm của đường chéo BC
⇒ \(\left\{{}\begin{matrix}H,M,K_{ }thẳng_{ }hàng\\HM=MK\end{matrix}\right.\)
Xét \(\Delta AHK\) có: \(\left\{{}\begin{matrix}AI=IK\left(gt\right)\\HM=MK\left(cmt\right)\end{matrix}\right.\)
⇒ \(IM\) là đường trung bình của \(\Delta AHK\)
⇒ \(IM=\dfrac{1}{2}AH\) \(\left(ĐPCM\right)\)
c)
Ta có:
\(\dfrac{S_{\Delta HBC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HD.BC}{\dfrac{1}{2}.AD.BC}=\dfrac{HD}{AD}\)
\(\dfrac{S_{\Delta HAC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HE.AC}{\dfrac{1}{2}.BE.AC}=\dfrac{HE}{BE}\)
\(\dfrac{S_{\Delta HBA}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HF.AB}{\dfrac{1}{2}.CF.AB}=\dfrac{HF}{CF}\)
⇒ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{\Delta HBC}+S_{\Delta HAC}+S_{\Delta HAB}}{S_{\Delta ABC}}=\dfrac{S_{\Delta ABC}}{S_{\Delta ABC}}\)
⇔ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\) \(\left(ĐPCM\right)\)