Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

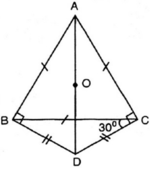
a) Theo giả thiết, =
=
.60o = 30o
=
+
(tia CB nằm giữa hai tia CA, CD)
=> = 60o + 30o = 90o (1)
Do DB = CD nên ∆BDC cân => =
= 30o
Từ đó = 60o + 30o = 90o (2)
Từ (1) và (2) có +
= 180o nên tứ giác ABDC nội tiếp được.
b) Vì = 90o nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.

Do tam giác ABC là tam giác nên A C B ^ = 60 o
=> Tứ giác ABDC có: ![]()
=> ABDC là tứ giác nội tiếp

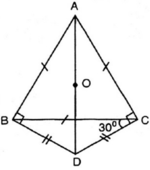
Ta có: A B D ^ = 90 o
⇒ AD là đường kính của đường tròn ngoại tiếp tam giác ABD Mà ABDC là tứ giác nội tiếp
⇒ AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC.
⇒ tâm O là trung điểm AD.
Vậy tâm đường tròn đi qua bốn điểm A, B, D, C là trung điểm AD.

a, ta có \(\widehat{ADB}\)là góc nội tiếp chắn nửa đường tròn => \(\widehat{ADB}=90^0\)hay \(\widehat{EDB}=90^0\)
Xét tứ giác BDEH có :
\(\widehat{EHB}=90^0\left(CH\perp AB\right)\)
\(\widehat{EDB}=90^0\left(cmt\right)\)
=> tugiac BDEH noi tiep
b,
ta có \(\widehat{ADC}=\widehat{ABC}\)( BDEH noitiep cmt)
mà \(\widehat{ABC}+\widehat{CAB}=90^0\)(góc ACB=90 độ, góc nt chắn nửa đg tròn)
\(\widehat{ACH}+\widehat{CAB}=90^0\)( góc AHC=90 độ vì CH vuông với AB)
=> \(\widehat{ABC}=\widehat{ACH}\)
=> \(\widehat{ACH}=\widehat{ADC}\left(=\widehat{ABC}\right)\)hay góc ADC= góc ACE
Xét tam giác ACE và tam giác ADC
\(\widehat{ADC}=\widehat{ACE}\left(cmt\right)\)
góc CAD chung
=> tam giác ACE đồng dạng với tam giác ADC (g-g)
=> \(\frac{AC}{AD}=\frac{AE}{AC}\)
=> \(AC^2=AD.AE\)(1)
Tam giác ABC vuông tại C có AH là đường cao
=> BC2= BH.BA (hethucluong) (2)
(1);(2) => \(AC^2+BC^2=AE.AD+BH.BA\)
mà AC2+ BC2= AB2 ( pytago trong tam giác ABC vuông ở C)
=> \(AB^2=AE.AD+BH.BA\)

⇒ AD là đường kính của đường tròn ngoại tiếp tam giác ABD Mà ABDC là tứ giác nội tiếp
⇒ AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC.
⇒ tâm O là trung điểm AD.
Vậy tâm đường tròn đi qua bốn điểm A, B, D, C là trung điểm AD.
Kiến thức áp dụng
+ Một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp được đường tròn.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.