K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

VV
18 tháng 4 2019
Xét tam giác QMC và tam giác NMB có:
BM=CN(giả thiết)
NM=NQ(GT)
BMN=QMC(đối đỉnh)
\(\Rightarrow\)2 tam giác = nhau
\(\Rightarrow\)QC=BN(2 cạnh tương ứng)
+)Ta có:N trung điểm AC
M trung điểm BC
Nên áp dụng bài toàn phụ về đường trung bình(ko biết thì nhớ search)
\(\Rightarrow\)MN//AB,MN=AB/2
\(\Rightarrow\)MQ//AB,MQ=AB/2(MN=MQ)
\(\Rightarrow\)MQ//AB,MQ=AP(AP=AB/2)
Ta có :MQ//AP<MQ=AP
Nên áp dụng tính chất đoạn chắn (tự search dùm nếu ko bít)
\(\Rightarrow\)AM=PQ.
(Kết luận thì tự đi mà viết mỏi tay VCL!!!)
Để phòng tránh copy ,vui lòng k cho vũ văn đạt đầu tiên
đường trung tuyến là đường đi qua trung điểm của đoạn thẳng đó
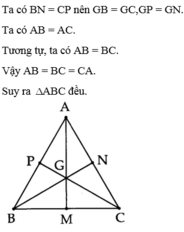
A B C M P N
tam giác ABC đều có 3 đường trung tuyến AM;BN;Cp suy ra các đoạn AP=PB=BM=MC=CN=NA
XÉT tam giác PMB và tam giác NMC có
PB = NC (cmt)
góc B = góc C (tam giác cân )
BM = Mc (cmt )
do đó tam giác PMB = tam giác NMC (c.g.c)
suy ra PM = MN (2 cạnh tương ứng )
xét tam giác PMB và tam giác PNA có
PA = PB (cmt)
BM = AN (cmt )
góc A = góc B (tam giác cân )
do đó tam giác PMB = tam giác PNA (c.g.c)
suy ra PN = PM (2 cạnh tuuwng ứng )
mà PM = MN suy ra PN = NM = MP
vậy tam giác MNP là tam giác cân\
Tam giác cân ư?