Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Áp dụng HTL2 vào tam giác ABC cuông tại A, đường cao AH ta có:
AH2=BH.HC=9.16=144
<=>AH=√144=12((cm)
Áp dụng định lý Pytago vào tam giác vuông BHA ta có:
BA2=AH2+BH2=122+92=225
<=>BA=√225=15(cm)
Áp dụng định lý Pytago vào tam giác vuông CHA ta có:
CA2=AH2+CH2=122+162=20(cm)
Vậy AB=15cm,AC=20cm,AH=12cm

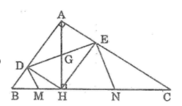
a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{ADH}=\widehat{AEH}=90^0\)
Do đó: ADHE là hình chữ nhật
a: Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>DE=AH=6cm
b: Gọi O là giao của AH và DE
=>O là trung điểm chung của AH và DE
mà AH=DE
nên OA=OH=OD=OE
Ta có: góc OHD+góc MHD=90 độ
góc ODH+góc MDH=90 độ
mà góc OHD=góc ODH
nên góc MHD=góc MDH
=>ΔMHD cân tại M và góc MDB=góc MBD
=>ΔMBD cân tại M
=>MH=MB
=>M là trung điểm của HB
Cm tương tự, ta được N là trung điểm của HC
=>MN=1/2BC
d: \(AD\cdot AB=AH^2\)
\(AE\cdot AC=AH^2\)
Do đó: \(AD\cdot AB=AE\cdot AC\)

ta có
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)
\(a+b-2\sqrt{ab}\ge0\)
\(a+b\ge2\sqrt{ab}\)
\(\frac{a+b}{2}\ge\sqrt{ab}\)
Ta có AH2=CH.BH=ab (1)
Gọi M là trung điểm của BC.
Xét tam giác AHM vuông tại H có AM là cạnh huyền --> AH\(\le\)AM (2)
Mà \(AM=\frac{BC}{2}=\frac{a+b}{2}\)(3)
Từ (1), (2) và (3) \(\Rightarrow a.b\le\frac{a+b}{2}\)