cho tam giác abc vuong tại a dường cao ah biết ab=5 ac=6 tính bc ah

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

TH

trần hoàng nam

8 tháng 9 2023

cho tam giác abc vuong tại a dường cao ah biết ab=5 ac=6 tính bc ah

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 9 2023

loading...

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TT

Tấn Thanh

4 tháng 6 2016 - olm

1. Cho tam giác ABC vuông tại A(AB<AC) có đường cao AH. Biết BC = 25cm, AH = 12cm. Tính AB, AC, BH, CH

2. Cho tam giác ABC vuồng tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính AC, BC, AH, BH

#Hỏi cộng đồng OLM #Toán lớp 8

0

DN

Dương Nguyễn Hoàng

20 tháng 2 2018 - olm

Cho tam giác ABC vuông tại A. Dường cao AH cắt đường phân giác BD tại I. BIết AB=6cm , AC= 8cm a, Tính BC b, Tính DB,DC c, chứng minh IA.BH = IH.BA

#Hỏi cộng đồng OLM #Toán lớp 8

0

LQ

Lại Quỳnh

25 tháng 3 2018 - olm

cho tam giác ABC vuông tại A , dường cao AH, có AB=6,AC=8 CK là tia phân giác của góc C,AH cắt CK tại E . tính diện tích tam giác HCE

#Hỏi cộng đồng OLM #Toán lớp 8

0

A

abcxyz300

18 tháng 8 2021

1.cho tam giác ABC vông tại A, đường cao AH. Biết AB=3cm, BC=5cm. Tính AC, AH, BH, CH 2. Cho tam giác ABC vông tại A, đường cao AH. Biết HB=3,6cm, HC=6,4cm. Tính BC,AB,AC,AH

#Hỏi cộng đồng OLM #Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

18 tháng 8 2021

Bài 1:

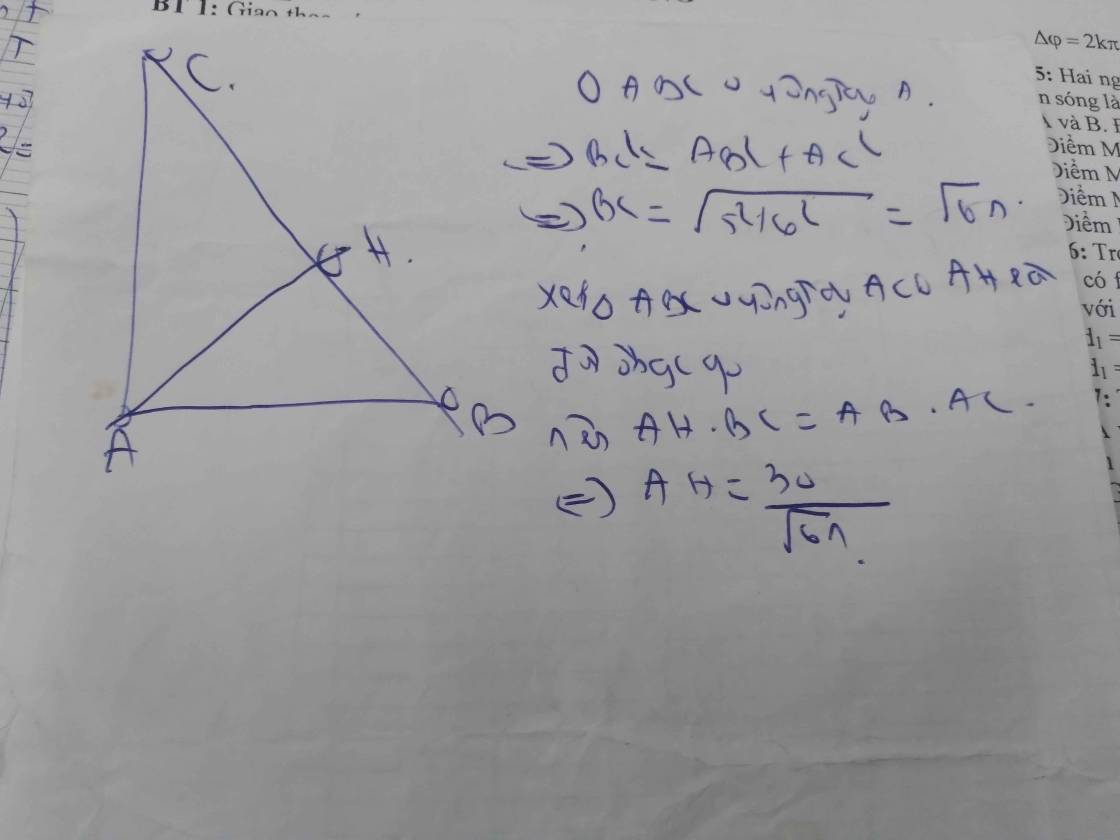
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow AC^2=5^2-3^2=16\)

hay AC=4cm

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH\cdot BC=AB\cdot AC\)

\(\Leftrightarrow AH\cdot5=3\cdot4=12\)

hay AH=2,4cm

NL

Nguyễn Lê Phước Thịnh

18 tháng 8 2021

Bài 2:

Ta có: BC=HB+HC

nên BC=3,6+6,4

hay BC=10cm

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=3.6\cdot10=36\\AC^2=6.4\cdot10=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+HB^2\)

\(\Leftrightarrow AH^2=6^2-3.6^2=23.04\)

hay AH=4,8cm

MR

Mostost Romas

6 tháng 4 2017 - olm

Giải giúp mình bài toán này với

Cho tam giác ABC vuông tại A, biết AB=3cm, AC=4cm, kẻ dường cao AH.

a) Cm: tam giác AHC đồng dạng tam giác BAC.

b) Tính BC, AH.

c) CM: HA^2=HC.HB

giải giúp mình câu c thôi

#Hỏi cộng đồng OLM #Toán lớp 8

1

VN

Vũ Như Mai

6 tháng 4 2017

Hình khỏi vẽ đi ha.

c/ Xét tam giác ABH và tam giác ACH có:

góc BHA = góc CHA = 90 độ (gt)

góc ABH = góc HAC (vì tam giác AHC đồng dạng tam giác BAC)

=> tam giác ABH đồng dạng tam giác ACH (g.g)

=> HA/HC = HB/HA

=> HA.HA = HB.HC

=> HA^2 = HB.HC

KU

Kim Uất Huyền

22 tháng 2 2020 - olm

Cho tam giác ABC vuông tại A, đường cao AH

a) Viết công thức tính diện tích tam giác ABC

b) Cho AB = 6 cm, BC = 10 cm. Tính AC, AH, DT tam giác ABC

#Hỏi cộng đồng OLM #Toán lớp 8

2

I

IS

22 tháng 2 2020

a) công thức . \(\frac{đáy.chiềucao}{2}\)

b) Áp dụng định lý pitago ta có

\(BC^2=AB^2+AC^2\)

=> AC^2=\(BC^2-AB^2=^{10^2}-6^2=64\)

=>\(AC=8\)

TP

Trịnh Phương Anh

22 tháng 2 2020

A)Xét tam giác ABC vuông tại A(gt),có:

SABC=(AB.AC)/2

B)Xét tam giác ABC vuông tại A(gt),có:

AB^2+AC^2=BC^2(ĐL Pytago)

Thay số:36+AC^×=100

<=>AC=căn64=8cm

Ta có:SABC=(AB.AC)/2

Thay số:SABC=24cm^2

Mà SABC=(AH.BC)/2

=>(AH.BC)/2=24

Thay số:AH=24.2:10=4,8cm

SABC=24CM^2(cmt)

B

Bruh

10 tháng 8 2021

Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AH = 6 cm; BH = 4,5 cm. Tính AB, AC, BC, HC.
b) Biết AB = 6 cm, BH = 3 cm. Tính AH, AC, CH

#Hỏi cộng đồng OLM #Toán lớp 8

1

MY

missing you =

10 tháng 8 2021

a,

pytago trong tam giác ABH

\(=>AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4,5^2}=7,5cm\)

dễ dàng chứng minh \(\Delta AHB\sim\Delta CAB\left(g.g\right)=>\dfrac{AH}{AC}=\dfrac{HB}{AB}=>AC=10cm\)

pytago cho tam giác ABC

\(=>BC=\sqrt{AB^2+AC^2}=12,5cm\)

\(=>HC=BC-HB=8cm\)

b, pytago cho tam giác AHB

\(=>AH=\sqrt{AB^2-BH^2}=3\sqrt{3}cm\)

rồi tính AC , CH làm tương tự bài trên

DD

dịch dương vương

23 tháng 4 2019 - olm

câu 2 : cho tam giác ABC vuông tại A có AB = 6 cm AC = 8 cm , đường cao AHa) chứng mính tam giác HBA đồng dạng tam giác ABCb) tính AHc) vẽ đường phân giác AD , tính BDd) trên AH lấy Q sao cho AQ = 1,8 cm , vẽ đường thẳng Q song song BC cắt AB , AC lần lượt tại I , K tính diện tích IKBC câu 1 cho tam giác ABC AB = 3 cm AC = 6 cm , trên AB , AC lần lượt lấy E , F sao cho AE = 2 cm AF = 4 cma) chứng minh EF song song BCb) tính BC...

#Hỏi cộng đồng OLM #Toán lớp 8

1

TT

Thị Trúc Uyên Mai

23 tháng 4 2019

câu 2:

a)xét tg HBA và ABC có

góc AHB=BAC=90⁰

góc B chung

=>tg HBA đồng dạng vs tg ABC(g-g)

b) áp dụng pytago vào tg ABC có

BC²=AB²+AC²

=>BC²=6²+8²

=>BC²=36+64

=>BC=\(\sqrt{100}=10cm\)

xét tam giác HBA đd vs tg ABC có

\(\frac{BA}{BC}=\frac{HA}{AC}\Rightarrow\frac{6}{10}=\frac{HA}{8}\Rightarrow HA=\frac{6.8}{10}\)

\(\Rightarrow HA=4,8\)

c) theo tính chất đường phân giác, ta có

\(\frac{BD}{DC}=\frac{AB}{AC}\Rightarrow\frac{BD}{DC}=\frac{6}{8}\Rightarrow\frac{BD}{BD+DC}=\frac{6}{8+6}\)

\(\Rightarrow\frac{BD}{BC}=\frac{6}{14}\)\(\Rightarrow\frac{BD}{10}=\frac{6}{14}\Rightarrow BD=\frac{6.10}{14}\approx4.3\)

DD

dịch dương vương

23 tháng 4 2019 - olm

câu 1 cho tam giác ABC AB = 3 cm AC = 6 cm , trên AB , AC lần lượt lấy E , F sao cho AE = 2 cm AF = 4 cma) chứng minh EF song song BCb) tính BC biết EF = 5 cmcâu 2 : cho tam giác ABC vuông tại A có AB = 6 cm AC = 8 cm , đường cao AHa) chứng mính tam giác HBA đồng dạng tam giác ABCb) tính AHc) vẽ đường phân giác AD , tính BDd) trên AH lấy Q sao cho AQ = 1,8 cm , vẽ đường thẳng Q song song BC cắt AB , AC lần lượt tại I , K tính...

#Hỏi cộng đồng OLM #Toán lớp 8

0