Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để giải bài toán này, ta có thể sử dụng các định lý và tính chất trong hình học Euclid. Dưới đây là cách chứng minh cho từng phần:
a) Chứng minh tam giác AIB = tam giác AIC:
Ta có AB = AC (do đề bài cho)IA = IA (do cùng là một đoạn)IB = IC (do I là trung điểm của BC)Vậy tam giác AIB và tam giác AIC bằng nhau theo nguyên lý cạnh - cạnh - cạnh.b) Chứng minh AI là tia phân giác của góc BAC:
Do tam giác AIB = tam giác AIC nên ∠BAI = ∠CAIVậy AI là tia phân giác của góc BAC.c) Chứng minh IA là tia phân giác của góc HIK:
Do IH vuông góc AB và IK vuông góc AC nên ∠HIK = 90° + ∠BACMà AI là tia phân giác của góc BAC nên ∠HIA = ∠KIA = 1/2 ∠BACVậy ∠HIA + ∠KIA = ∠HIKVậy IA là tia phân giác của góc HIK.a: Xét ΔAIB và ΔAIC có
AB=AC
IB=IC
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của \(\widehat{BAC}\)
c: Xét ΔAIH vuông tại H và ΔAIK vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAIH=ΔAIK
=>\(\widehat{HIA}=\widehat{KIA}\)
=>IA là phân giác của \(\widehat{HIK}\)

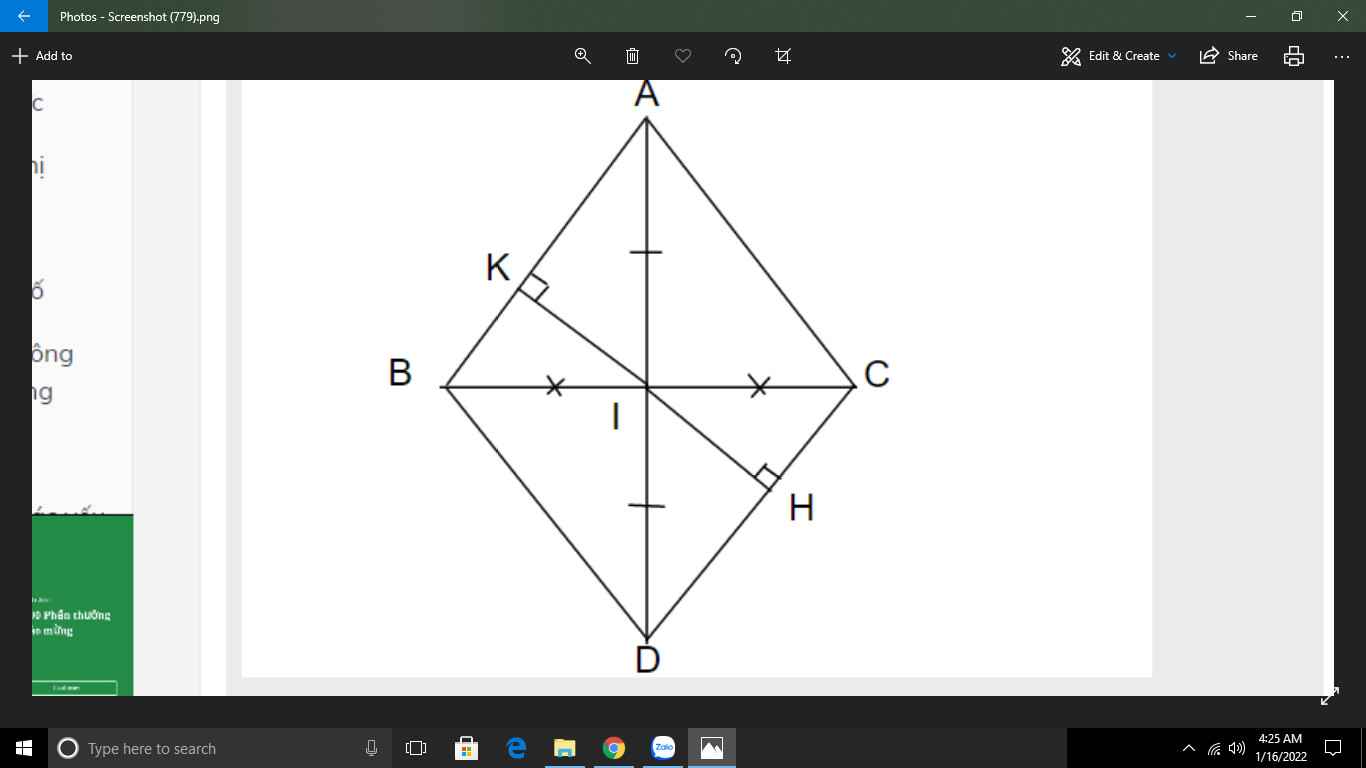
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o
Mà BI và CI lâ các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) + 2.∠(ICB) = 2 (∠(IBC) + ∠(ICB) )
Suy ra ∠(IBC) + ∠(ICB) = 50o
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o.

C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm

Ta có hình vẽ:
A B C I H K
a/ Xét tam giác AIB và tam giác AIC có:
BI = IC (GT)
\(\widehat{AIB}\)=\(\widehat{AIC}\) (AI là đường trung trực của BC)
AI : cạnh chung
Vậy tam giác AIB = tam giác AIC (c.g.c)
b/ Ta có: tam giác AIB = tam giác AIC (câu a)
=> \(\widehat{BAI}\)=\(\widehat{CAI}\) (2 góc tương ứng)
=> AI là phân giác \(\widehat{BAC}\) (đpcm)
c/
*Cách 1:
Xét tam giác AHI và tam giác AKI có:
\(\widehat{AHI}\)=\(\widehat{AKI}\) = 900
AI: cạnh chung
\(\widehat{HAI}\)=\(\widehat{KAI}\) (đã chứng minh)
Vậy tam giác AHI = tam giác AKI
(theo trường hợp cạnh huyền góc nhọn)
=> IH = IK (2 cạnh tương ứng)
*Cách 2:
Xét tam giác BHI và tam giác CKI có:
\(\widehat{B}\)=\(\widehat{C}\) (vì tam giác AIB = tam giác AIC)
BI = IC (GT)
\(\widehat{BHI}\)=\(\widehat{CKI}\)=900
Vậy tam giác BHI = tam giác CKI
(theo trường hợp cạnh huyền góc nhọn)
=> IH = IK (2 cạnh tương ứng)
Ở đây mình làm 2 cách nhưng khi vào làm bài bạn viết 1 cách thôi nhé, bạn chọn cách nào dễ hiểu mà làm...^^
đề bài sai bn ơi
ih vuông góc vs ac
vậy làm sao