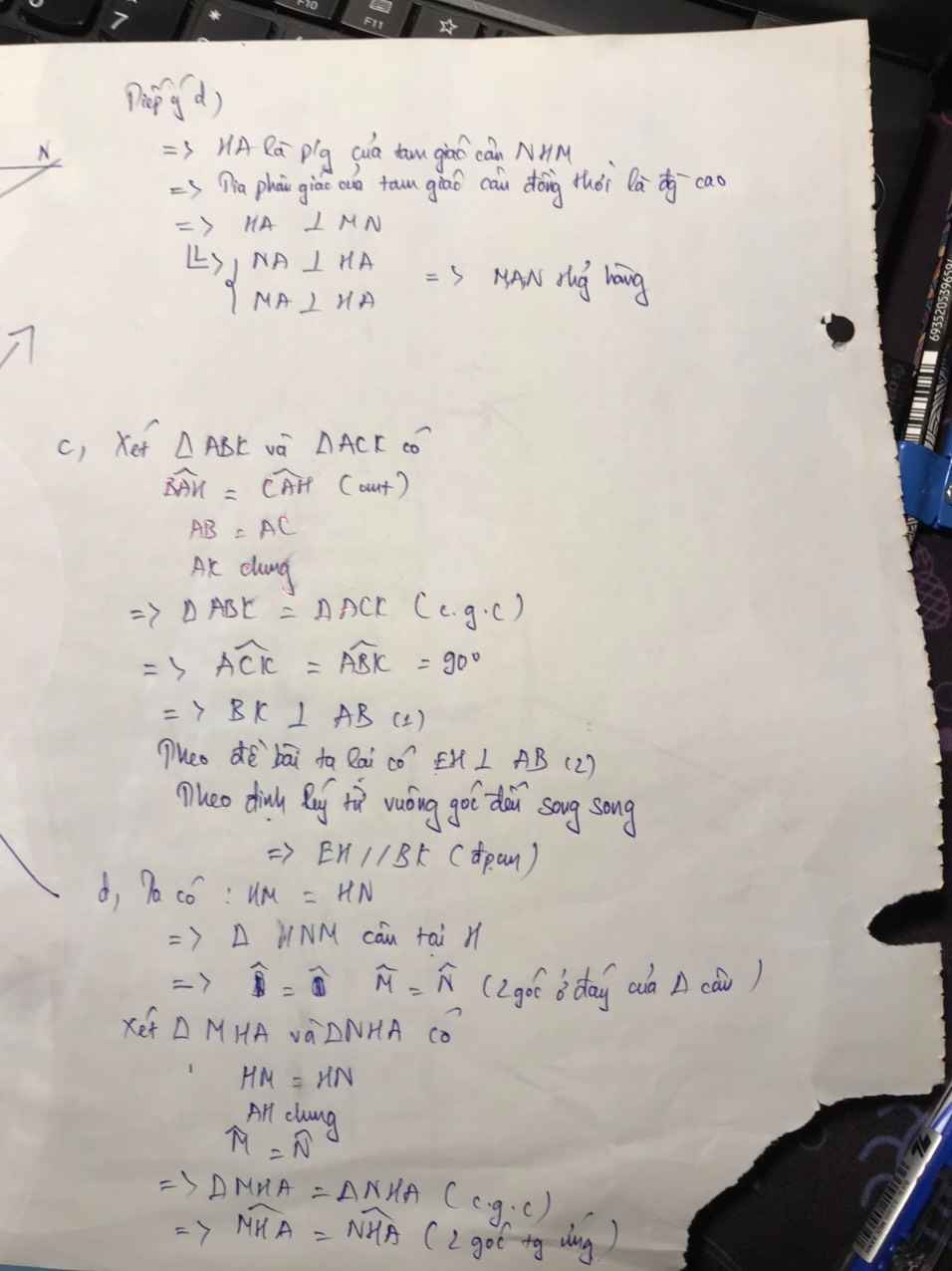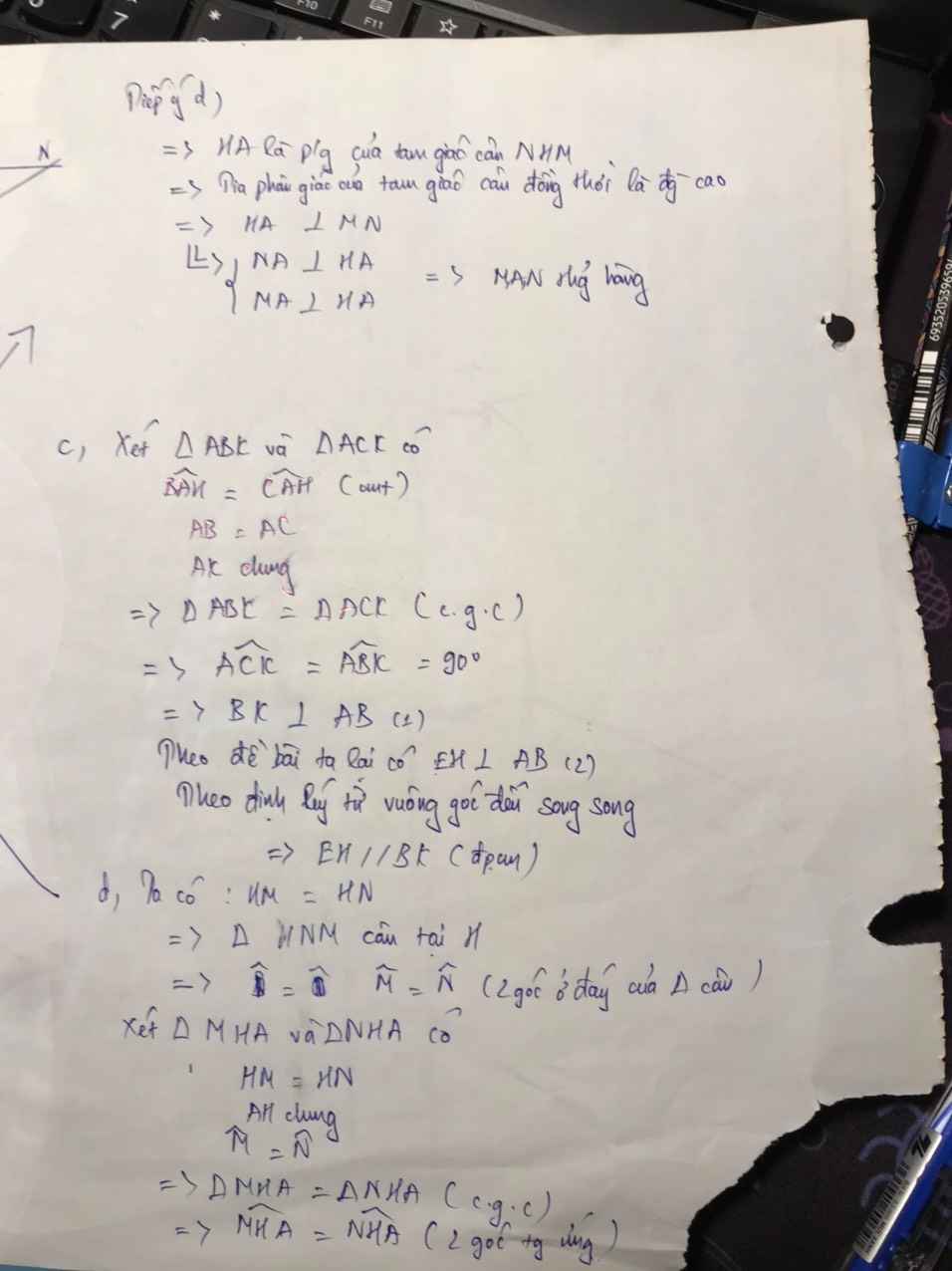Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAHM có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM(1)
Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc HAN(2)
Từ (1) và (2) suy ra \(\widehat{MAN}=\widehat{MAH}+\widehat{NAH}=2\cdot\widehat{BAC}=180^0\)
hay M,A,N thẳng hàng
Xét ΔAHB và ΔAMB có
AH=AM
\(\widehat{BAH}=\widehat{MAH}\)
AH chung
Do đó: ΔAHB=ΔAMB
Suy ra: \(\widehat{AHB}=\widehat{AMB}=90^0\)
hay BM\(\perp\)MA
hay BM\(\perp\)MN(3)
Xét ΔAHC và ΔANC có
AH=AN
\(\widehat{HAC}=\widehat{NAC}\)
AC chung
Do đó: ΔAHC=ΔANC
Suy ra: \(\widehat{AHC}=\widehat{ANC}=90^0\)
hay CN\(\perp\)NA
=>CN\(\perp\)NM(4)
Từ(3) và (4) suy ra MB//NC

a: Xét ΔAMH có
AE là đường cao
AE là đường trug tuyến
Do đó: ΔAMH cân tại A
hay AM=AN
b: Xét ΔHBM có
BE là đường cao
BE là đường trung tuyến
Do đó:ΔHBM cân tại B
hay BH=BM
Xét ΔAHB và ΔAMB có
AH=AM
HB=MB
AB chung
Do đó: ΔAHB=ΔAMB
Suy ra: \(\widehat{AHB}=\widehat{AMB}=90^0\)
c: Ta có: ΔAHM cân tại A
mà AB là đường cao
nên AB là tia phân giác của góc HAM(1)
Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
DO đó: ΔAHN cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc HAN(2)
Từ (1) và (2) suy ra \(\widehat{MAN}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=180^0\)
=>M,A,N thẳng hàng
mà AM=AN(=AH)
nên A là trung điểm của MN

ĐỀ QUẬN BÌNH TÂN NĂM 2016 - 2017
a) Xét \(\Delta ABH\)và \(\Delta ACH\)ta có:
AH là cạnh chung
AB = AC ( \(\Delta ABC\)cân tại A)
BH = CH ( H là trung điểm của BC)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c-c-c\right)\)
Xét \(\Delta ABC\)cân tại A ta có:
AH là đường trung tuyến ( H là trung điểm của BC)
\(\Rightarrow\)AH là đường cao của \(\Delta ABC\)
\(\Rightarrow AH⊥BC\)tại H.
b) Xét \(\Delta BDH\)vuông tại D và \(\Delta CEH\)vuông tại E ta có:
BH = CH ( H là trung điểm của BC)
\(\widehat{DBH}=\widehat{ECH}\)(\(\Delta ABC\)cân tại A)
\(\Rightarrow\Delta BDH=\Delta CEH\left(ch-gn\right)\)
\(\Rightarrow\)BD = CE ( 2 cạnh tương ứng)
c) Ta có:
AB = AC (\(\Delta ABC\)cân tại A)
BD = CE ( cmt)
\(\Rightarrow AB-BD=AC-CE\)
\(\Rightarrow AD=AE\)
\(\Rightarrow\Delta ADE\)cân tại A
\(\Rightarrow\widehat{ADE}=\frac{180^o-\widehat{DAE}}{2}\)
Mà \(\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\)
Nên \(\widehat{ADE}=\widehat{ABC}\)
Mặt khác 2 góc này nằm ở vị trí đồng vị
\(\Rightarrow\)DE // BC.
d) Nối A với I.
Ta có:
\(\hept{\begin{cases}HE=HM+ME\left(M\in HE\right)\\HM=EN\left(gt\right)\end{cases}}\)
\(\Rightarrow HE=EN+ME\)
\(\Rightarrow HE=MN\)
Xét \(\Delta AEN\)vuông tại E ta có:
\(\hept{\begin{cases}AN^2=AE^2+EN^2\left(Pitago\right)\\AE=AD\left(cmt\right)\\EN=HM\left(gt\right)\end{cases}}\)
\(\Rightarrow AN^2=AD^2+HM^2\)
\(\Rightarrow AN^2=AD^2+HI^2-MI^2\)
\(\Rightarrow AN^2=AD^2+HI^2-\left(NI^2-MN^2\right)\)
\(\Rightarrow AN^2=AD^2+HI^2-NI^2+HD^2\)
\(\Rightarrow AN^2=AD^2+HD^2+HI^2-NI^2\)
\(\Rightarrow AN^2=AH^2+HI^2-NI^2\)
\(\Rightarrow AN^2=AI^2-NI^2\)
\(\Rightarrow AI^2=AN^2+NI^2\)
\(\Rightarrow\Delta ANI\)vuông tại N ( Định lý Pitago đảo)
\(\Rightarrow IN⊥AN\)tại N.