Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu b
Từ N kể đường thẳng song song với BC cắt đường thẳng AB tại K => KBCN là hình thang (*)
Lại có góc BKN = ABC ( đồng vị), CNK = ACB (đồng vị) và ABC = ACB nên BKN = CNK (**)
từ (*) và (**) => KBCN là hình thang cân => BK = CN = BM.
=> AK = AN nên tam giác AKN cân tại A => AO là đường trung trực của KN => OK = ON (4)
vì OI là trung trực của MN nên OM = ON (5)
từ (4) và (5) => OM = OK => tam giác OMK cân tại O lại có BM = BK (cmt) nên OB v^g góc với AB.
Tam giác ABO và Tam giác ACO có: AB = ÃC, BAO = CAO (gt) , AO chung nên tam giác ABO = tam giác ACO (c,g,c) => ACO = ABO = 90độ. hay OC vuông góc với AC.

- Vẽ tam giác ABC:
- Vẽ tam giác nhọn ABC sao cho \(A B < A C\).
- Vẽ đường tròn (O) nội tiếp tam giác này.
- Lấy các điểm D và E:
- Trên tia \(B A\), lấy điểm D sao cho \(B D = C E\).
- Trên tia \(C A\), lấy điểm E sao cho \(B D = C E\).
- Vẽ tam giác ADE:
- Nối D và E với A để tạo thành tam giác ADE.
- Vẽ đường tròn ngoại tiếp tam giác ADE:
- Vẽ đường tròn ngoại tiếp tam giác ADE. Đường tròn này sẽ cắt đường tròn (O) tại điểm K khác A.
- Điểm K:
- Điểm K là điểm giao của đường tròn ngoại tiếp của tam giác ADE và đường tròn (O).

cho A=1+2+22+.........+22009+22010.Tìm số dư khi chia a cho 7

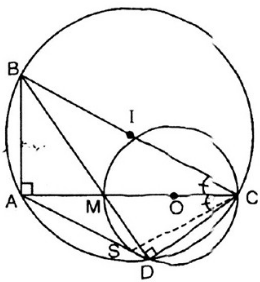
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB