K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

27 tháng 7 2023
Sửa đề: CM A,M,N thẳng hàng
Xét ΔABD có
BC là trung tuýen
BM=2/3BC
=>M là trọng tâm
mà N là trung điểm của BD
nên A,M,N thẳng hàng

16 tháng 4 2019
Tự vẽ hình
Ta có:
AMB=CMN(2 góc đối đỉnh)
AMC=BMN(2 góc đối đỉnh)
Mà AMB+AMC=180
BMN+MNC=180
=> AMB+BMN=180
=>3 điểm A,M,N thẳng hàng

K
2 tháng 3
- Chứng minh ∆ADE = ∆ABC:
Dùng tiêu chí Cạnh-Góc-Cạnh vì:- \(A B = A D\) (A là trung điểm của BD).
- \(A C = A E\) (A là trung điểm của CE).
- \(\angle B A C = \angle D A E\) (góc đối đỉnh).
- Chứng minh DE // BC:
Vì \(\Delta A D E = \Delta A B C\) (theo C-G-C), nên:
\(\angle A D E = \angle A B C\) và \(\angle D E A = \angle A C B\).
→ DE // BC theo định lý góc đồng vị. - Chứng minh M, A, N thẳng hàng:
M, N lần lượt là trung điểm của DE và BC nên AM là đường trung bình của tam giác lớn. Đường trung bình đi qua trung điểm nối song song với cạnh còn lại nên M, A, N thẳng hàng.
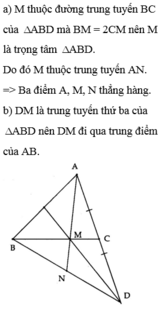

Xét ΔABD có
BC là trung tuyến
BM=2/3BC
=>M là trọng tâm
=>A,M,N thẳng hàng