Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔABC vuông tại A
=>\(\hat{ABC}+\hat{ACB}=90^0\)
=>\(\hat{ACB}=90^0-65^0=25^0\)
ΔHAC vuông tại H
=>\(\hat{HAC}+\hat{HCA}=90^0\)
=>\(\hat{HAC}=90^0-25^0=65^0\)
HD là phân giác của góc AHC
=>\(\hat{AHD}=\hat{CHD}=\frac12\cdot\hat{AHC}=45^0\)
Xét ΔCDH có \(\hat{ADH}\) là góc ngoài tại đỉnh D
nên \(\hat{ADH}=\hat{DCH}+\hat{DHC}=25^0+45^0=70^0\)

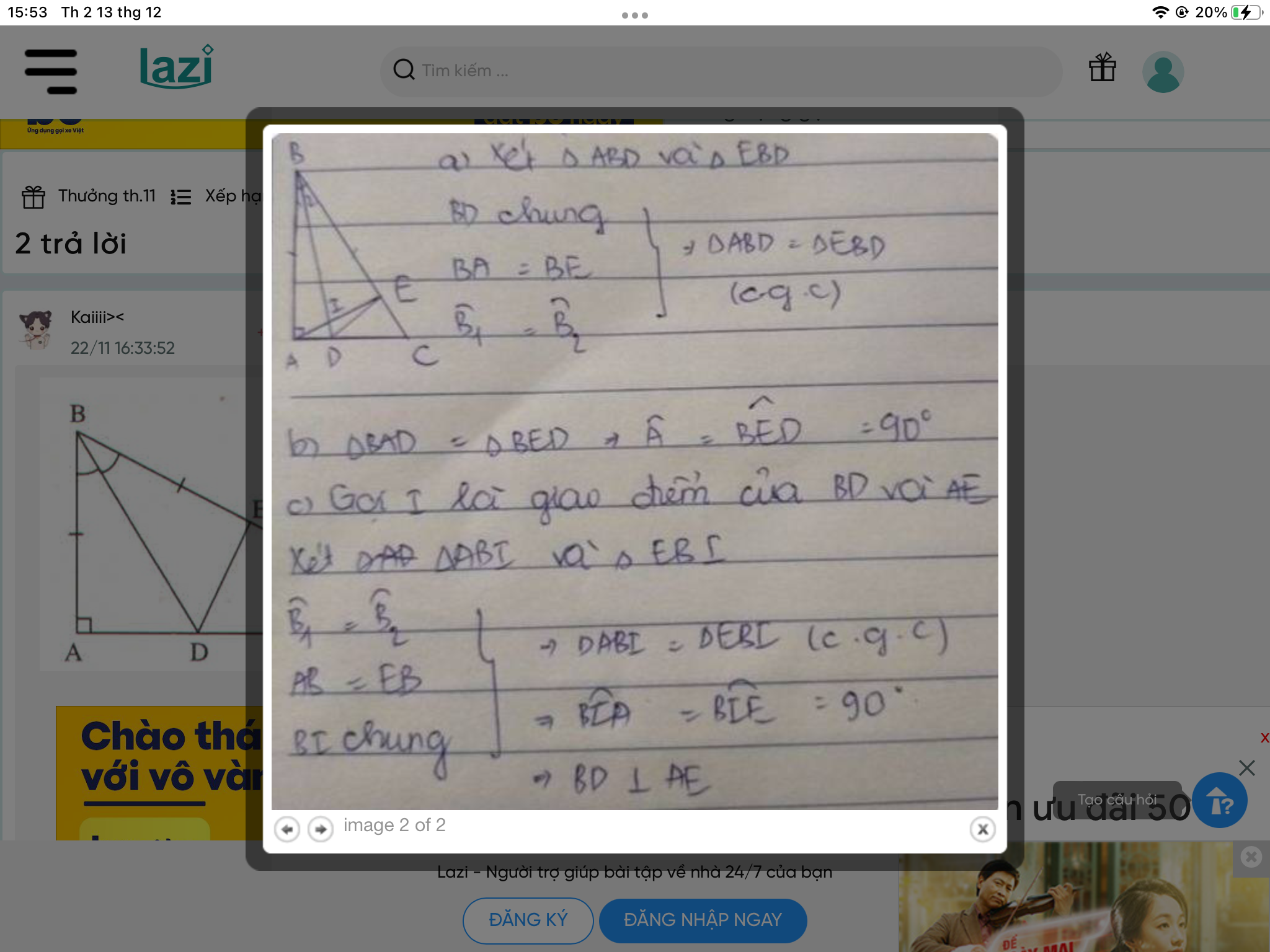
Bạn tự vẽ hình nha ^^
a)--- Xét \(\Delta ABD\)và \(\Delta EBD\)có
\(AB=EB\left(GT\right)\)(1)
\(\widehat{BAD}=\widehat{BED}=90^o\)(2)
\(BD:\)Cạnh chung (3)
Từ (1) ;(2) và (3)
\(\Rightarrow\Delta ABD=\Delta EBD\)( c.g.c )
b)
---Theo đề bài ta có :
\(AB=EB\left(GT\right)\)(1)
và \(\widehat{ABC}=60^o\left(gt\right)\)(2)
Từ (1)và (2)\(\Rightarrow\Delta ABE\)đều (đpcm)
--- Vì \(\Delta ABE\)đều
\(\Rightarrow AB=BE=AE\)
Mà \(AB=6cm\)(gt)
...\(AE=EC\)
\(\Rightarrow EC=6cm\)
mà \(BE=6cm\)
Có \(EC+BE=BC\)
\(\Rightarrow6+6=12cm\)
Vậy BC =12cm

a ) Vì CM là tia phân giác của góc KCH
\(\Rightarrow\)Góc KCM = Góc HCM = 50° / 2 = 25°
Trong \(\Delta\)CHM có :
Góc MHC + Góc CMH + Góc MCH = 180°
\(\Leftrightarrow\)90° + Góc CMH + 25° = 180°
\(\Leftrightarrow\)Góc CMH = 65°
b ) Xét \(\Delta\)CMK và \(\Delta\)CMH có :
- CK = CH ( giả thiết )
- Góc KCM = Góc HCM ( vì CM là tia phân giác của góc KCH )
- MC : cạnh chung
\(\Rightarrow\)\(\Delta\)CMK = \(\Delta\)CMH ( C - G - C )
\(\Rightarrow\)MK = MH ( 2 cạnh tương ứng )
c ) Ta có : MK = MH ( cmt )
\(\Rightarrow\)M nằm trên đường trung trực của KH ( 1 )
Ta lại có : CK = CH ( giả thiết )
\(\Rightarrow\)C nằm trên đường trung trực của KH ( 2 )
Từ ( 1 ) và ( 2 ), suy ra MC là đường trung trực của KH
\(\Rightarrow\)MC \(\perp\)KH
d ) Ta có : Góc KCH + Góc HCN = 90° ( vì NC \(\perp\)KC )
\(\Rightarrow\)Góc KCM + Góc HCM + Góc HCN = 90°
\(\Rightarrow\)25° + Góc NCM = 90°
\(\Rightarrow\)Góc NCM = 65°
Mà ta có : Góc NMC = 65°
\(\Rightarrow\)Góc NCM = Góc NMC

ΔABC vuông tại A
=>\(\hat{B}+\hat{C}=90^0\)
mà \(\hat{B}-\hat{C}=\alpha\)
nên \(\hat{B}=\frac{90^0+\alpha}{2}\)
AD là phân giác của góc BAC
=>\(\hat{BAD}=\hat{CAD}=\frac{90^0}{2}=45^0\)
Ta có: \(\hat{BAH}+\hat{B}=90^0\)
=>\(\hat{BAH}=90^0-\hat{B}=90^0-\frac{90^0+\alpha}{2}=\frac{90^0-\alpha}{2}=45^0-\frac12\cdot\alpha\)
Vì \(\hat{BAH}<\hat{BAD}\)
nên tia AH nằm giữa hai tia AB và AD
=>\(\hat{BAH}+\hat{HAD}=\hat{BAD}\)
=>\(\hat{HAD}=45^0-\left(45^0-\frac12\cdot\alpha\right)=\frac12\cdot\alpha\)