Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

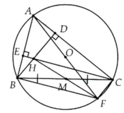
a,Chứng minh được BFCH là hình bình hành
b, Sử dụng kết quả câu a), suy ra HF đi qua M
c, Chú ý: OM là đường trung bình của ∆AHF => ĐPCM

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB đồng dạng với ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
b: Xét (O) có
ΔABF nội tiếp
AF là đường kính
Do đó: ΔABF vuông tại B
=>BF vuông góc AB
mà CH vuông góc AB
nên BF//CH
Xét (O) có
ΔACF nội tiếp
AF là đường kính
Do đó: ΔACF vuông tại C
=>AC vuông góc CF
mà AC vuông góc BH
nên BH//CF
Xét tứ giác BHCF có
BH//CF
BF//CH
Do đó: BHCF là hình bình hành
c: BHCF là hình bình hành
=>BC cắt HF tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HF
=>H,M,F thẳng hàng

a: Xét (O) có
ΔABK nội tiếp
AK là đường kính
Do đó: ΔABK vuông tại B
=>BK vuông góc với AB
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
=>AC vuông góc với CK
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: Vì BHCK là hình bình hành
nên BC cắt HK tại trung điểm của mỗi đường
=>M là trung điểm của HK
Xét ΔKAH có
KO/KA=KM/KH
nên OM//AH và OM/AH=KO/KA=1/2
=>OM=1/2AH

a: Xét (O) có
ΔABF nội tiếp
AF là đường kính
Do đo: ΔABF vuông tại B
=>BF//CH
Xét (O) có
ΔACF nội tiếp
AF là đường kính
Do đo: ΔACF vuông tại C
=>CF//BH
mà BF//CH
nên BFCH là hình bình hành
b: Vì BFCH là hình bình hành
nên BC cắt FH tại trung điểm của mỗi đường
=>H,M,F thẳng hàng
a) \(\widehat{ACF}=90^0\) ( chắn nửa đường tròn ) => FC vuông góc với AC
Lại có BH vuông góc với AC => FC // BH (1)
Chứng minh tương tự: BF // CH (2)
Từ (1) và (2) => BFCH là hình bình hành.
b) Vì BFCH là hình bình hành nên 2 đường chéo HF và BC giao nhau tại trung điểm mỗi đường.
Mà M là trung điểm của BC => M đồng thời là trung điểm của HF
=> H, M, F thẳng hàng ( đpcm )
c) Xét tam giác AHF có O là trung điểm của AF
Có M là trung điểm của HF => OM là đường trung điểm của tam giác AHF
=> OM = \(\frac{1}{2}\) AH ( đpcm )
Đường trung bình nhaaaaa