Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do BE và CF là các đường cao trong tam giác ABC nên ˆBEC=90∘, ˆBFC=90∘
Tứ giác BCEF có góc E và góc F cùng nhìn cạnh BC và bằng nhau (cùng bằng 90∘) nên là tứ giác nội tiếp.
b) Tứ giác BCEF là tứ giác nội tiếp nên ˆAFE=ˆACB, mà ˆACB=ˆASB (cùng chắn cung AB) nên ˆAFE=ˆASB
Suy ra tứ giác BFMS là tứ giác nội tiếp.
Do đó ˆFMS=180∘−ˆFBS=90∘.. Vậy OA ⊥⊥ EF.
c)
+) Tứ giác BCEF nội tiếp nên ˆAEF=ˆABC (1)
Từ OA ⊥ PE suy ra ˆAIB=ˆAPE(cùng phụ với ˆMAP). (2)
Từ (1) và (2) suy ra ΔAPE∽ΔABI (g.g).
+) Tứ giác BHCS có BH // CS (cùng vuông góc với AS) và BS // CH (cùng vuông góc với AB) nên là hình bình hành. Do đó ba điểm H, K, S thẳng hàng.
Ta sẽ chứng minh hai góc đồng vị ˆPIM và HSM^ bằng nhau.
Tứ giác PDIM nội tiếp (vì có hai góc vuông M và D đối nhau) nên ˆPIM=ˆPDM (3)
Ta có:
ΔAHE∽ΔACDΔ nên AH.AD = AE.AC.
ΔAME∽ΔACSnên AM.AS = AE.AC.
Suy ra AH.AD = AM.AS ⇒AH/AM=AS/AD.
Do đó ΔMAH∽ΔDAS(c.g.c). Suy ra AHM^=ASD^.
Từ đó ta có tứ giác DHMS là tứ giác nội tiếp. Suy ra ˆHDM=ˆHSM. (4)
Từ (3) và (4) suy ra HS // PI, hay KH // PI.

Câu 8:
a) Xét tứ giác BFEC có
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

A B C O E F K I J H M N S T L
c) AT là đường kính của (O), dễ thấy H,K,T thẳng hàng, gọi TH cắt (O) lần nữa tại S, ta được ^ASH = 900
Ta có A,E,H,F,S cùng thuộc đường tròn đường kính AH, suy ra:
(ES,EF) = (AS,AB) = (SC,SB), (SF,SE) = (BS,BC) do đó \(\Delta\)SFE ~ \(\Delta\)SBC
Vì K,L là trung điểm của BC,EF nên \(\Delta\)SFL ~ \(\Delta\)SBK, suy ra \(\Delta\)SFB ~ \(\Delta\)SLK, (KS,KL) = (BS,BA) (1)
Lại có: \(\frac{MF}{MB}=\frac{HF}{HB}=\frac{HE}{HC}=\frac{NE}{NC}\), \(\Delta\)SEC ~ \(\Delta\)SFB, suy ra \(\Delta\)SMN ~ \(\Delta\)SBC
Tương tự như trên, ta thu được (KS,KI) = (BS,BA) (2)
Từ (1);(2) suy ra K,I,L thẳng hàng. Mặt khác K,L,J thẳng hàng vì chúng cách đều E,F.
Do vậy I,J,K thẳng hàng.

1: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
2: Xét ΔKBF và ΔKEC có
góc KBF=góc KEC
góc K chung
=>ΔKBF đồng dạng với ΔKEC
=>KB/KE=KF/KC
=>KB*KC=KE*KF

Bài 1:
A B C H F D E K L
+) Chứng minh tứ giác BFLK nội tiếp:
Ta thấy FAH và LAH là hai tam giác vuông có chung cạnh huyền AH nên AFHL là tứ giác nội tiếp. Vậy thì \(\widehat{ALF}=\widehat{AHF}\) (Hai góc nội tiếp cùng chắn cung AF)
Lại có \(\widehat{AHF}=\widehat{FBK}\) (Cùng phụ với góc \(\widehat{FAH}\) )
Vậy nên \(\widehat{ALF}=\widehat{FBK}\), suy ra tứ giác BFLK nội tiếp (Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
+) Chứng minh tứ giác CELK nội tiếp:
Hoàn toàn tương tự : Tứ giác AELH nội tiếp nên \(\widehat{ALE}=\widehat{AHE}\) , mà \(\widehat{AHE}=\widehat{ACD}\Rightarrow\widehat{ALE}=\widehat{ACD}\)
Suy ra tứ giác CELK nội tiếp.

Giải chi tiết:
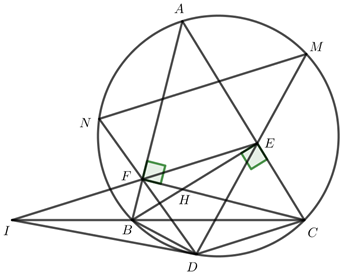
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

Bài toán: Cho tam giác \(A B C\) nhọn nội tiếp đường tròn \(\left(\right. O \left.\right)\). Gọi \(B E\), \(C F\) lần lượt là các đường cao của tam giác \(A B C\), cắt nhau tại \(H\). Gọi \(K\) là trung điểm của \(B C\). Chứng minh:
a) Tam giác \(A E F\) đồng dạng với tam giác \(A B C\).
b) Chứng minh \(O A\) vuông góc với \(E F\).
Giải:
a) Chứng minh tam giác \(A E F\) đồng dạng với tam giác \(A B C\)
Để chứng minh hai tam giác \(A E F\) và \(A B C\) đồng dạng, ta cần chỉ ra rằng các góc của chúng tương ứng bằng nhau hoặc tỉ lệ giữa các cạnh tương ứng bằng nhau.
Cách tiếp cận:
Do \(A E F\) là tam giác con được tạo bởi các đường cao của tam giác \(A B C\), và \(A E F\) chia góc của tam giác \(A B C\), ta sẽ sử dụng định lý góc đồng dạng (hoặc tỉ lệ cạnh đồng dạng) để kết luận rằng \(\triangle A E F sim \triangle A B C\).
Các góc của tam giác \(A E F\) tương ứng với các góc trong tam giác \(A B C\), cụ thể:
Vậy, \(\triangle A E F sim \triangle A B C\) theo tiêu chuẩn góc-góc-góc (g-g-g).
b) Chứng minh \(O A\) vuông góc với \(E F\)
Để chứng minh \(O A\) vuông góc với \(E F\), ta sẽ sử dụng tính chất của trực tâm và những định lý liên quan đến đường tròn nội tiếp.
Cách tiếp cận:
Vì tam giác \(A B C\) là tam giác nhọn, các đường cao \(B E\) và \(C F\) sẽ cắt nhau tại trực tâm \(H\), đồng thời cũng vuông góc với các cạnh của tam giác.
Do đó, \(O A\) vuông góc với \(E F\).
Kết luận:
a) Tam giác \(A E F\) đồng dạng với tam giác \(A B C\).
b) \(O A\) vuông góc với \(E F\).
4o miniBài toán: Cho tam giác \(A B C\) nhọn nội tiếp đường tròn \(\left(\right. O \left.\right)\). Gọi \(B E\), \(C F\) lần lượt là các đường cao của tam giác \(A B C\), cắt nhau tại \(H\). Gọi \(K\) là trung điểm của \(B C\). Chứng minh:
a) Tam giác \(A E F\) đồng dạng với tam giác \(A B C\).
b) Chứng minh \(O A\) vuông góc với \(E F\).
Giải:
a) Chứng minh tam giác \(A E F\) đồng dạng với tam giác \(A B C\)
Để chứng minh hai tam giác \(A E F\) và \(A B C\) đồng dạng, ta cần chỉ ra rằng các góc của chúng tương ứng bằng nhau hoặc tỉ lệ giữa các cạnh tương ứng bằng nhau.
Cách tiếp cận:
Do \(A E F\) là tam giác con được tạo bởi các đường cao của tam giác \(A B C\), và \(A E F\) chia góc của tam giác \(A B C\), ta sẽ sử dụng định lý góc đồng dạng (hoặc tỉ lệ cạnh đồng dạng) để kết luận rằng \(\triangle A E F s i m \triangle A B C\).
Các góc của tam giác \(A E F\) tương ứng với các góc trong tam giác \(A B C\), cụ thể:
Vậy, \(\triangle A E F s i m \triangle A B C\) theo tiêu chuẩn góc-góc-góc (g-g-g).
b) Chứng minh \(O A\) vuông góc với \(E F\)
Để chứng minh \(O A\) vuông góc với \(E F\), ta sẽ sử dụng tính chất của trực tâm và những định lý liên quan đến đường tròn nội tiếp.
Cách tiếp cận:
Vì tam giác \(A B C\) là tam giác nhọn, các đường cao \(B E\) và \(C F\) sẽ cắt nhau tại trực tâm \(H\), đồng thời cũng vuông góc với các cạnh của tam giác.
Do đó, \(O A\) vuông góc với \(E F\).
Kết luận:
a) Tam giác \(A E F\) đồng dạng với tam giác \(A B C\).
b) \(O A\) vuông góc với \(E F\).