Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BC\) \(\subset\)\(\left(SBC\right)\)
Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):
\(N\)là điểm chung thứ nhất
Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)
\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)
Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)
\(K\)là điểm chung thứ 2.
Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)
Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)
Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)
Ta có N thuộc (OMN)
C thuộc đường thẳng BC
Mà N trùng với C => N là giao điểm của (OMN) và BC

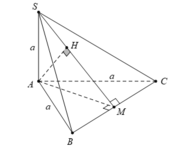
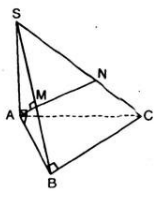
● Gọi M là trung điểm của BC ; H là hình chiếu vuông góc của A trên SM.
● Vì tam giác ABC đều nên: BC ⊥ AM.
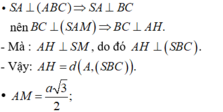
- Trong tam giác vuông SAM, đường cao AH có:
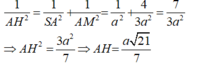

Lời giải:
Gọi $K$ là giao điểm của đường thẳng $a$ với $AB$ thì $A'K\subset (A',a)$
Ta thấy: $K\in AB; A'\in SA\Rightarrow A'K\subset (SAB)$
Do đó $A'K$ là giao tuyến của $(A',a)$ và $(SAB)$
Giao tuyến với các mặt phẳng $(SAC,SBC)$ bạn thực hiện tương tự.

1:
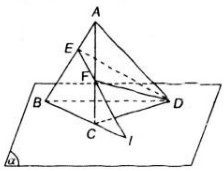
a: \(D\in SA\subset\left(SAB\right);E\in SB\subset\left(SAB\right)\)
Do đó: \(DE\subset\left(SAB\right)\)
b: \(F\in AB\subset\left(SAB\right)\)
\(F\in DE\subset\left(CDE\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(CDE\right)\)
2:
\(N\in AB\subset\left(ABM\right);N\in CD\subset\left(SCD\right)\)
Do đó: \(N\in\left(ABM\right)\cap\left(SCD\right)\)
\(M\in SC\subset\left(SCD\right);M\in MB\subset\left(ABM\right)\)
Do đó: \(M\in\left(ABM\right)\cap\left(SCD\right)\)
Do đó: \(\left(ABM\right)\cap\left(SCD\right)=MN\)

Tham khảo:
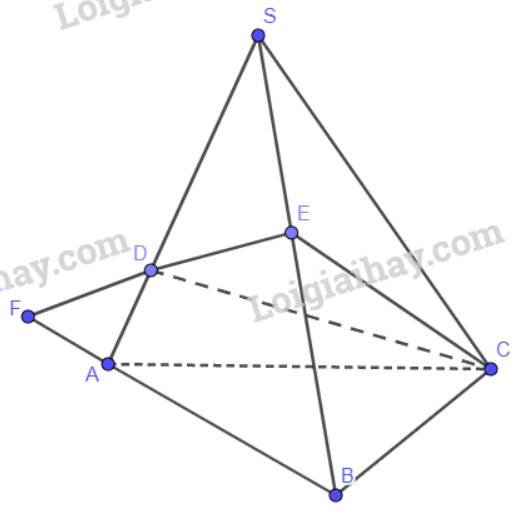
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).

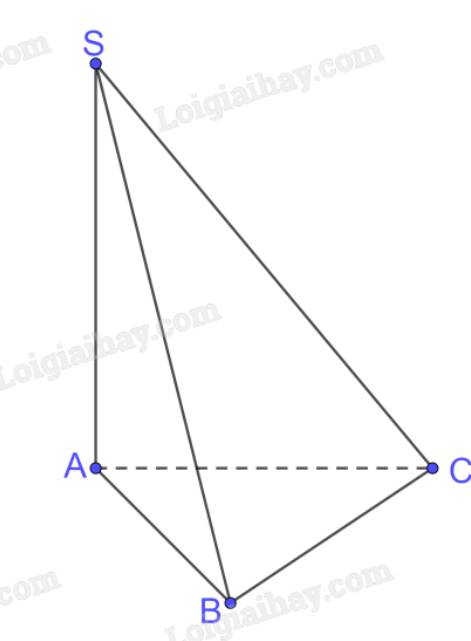
a) Ta có SA \( \bot \) (ABC) nên A là hình chiếu của S trên (ABC)
b) A là hình chiếu của S trên (ABC)
B là hình chiếu của B trên (ABC)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) Tam giác ABC là hình chiếu của tam giác SBC.
c) B là hình chiếu của C trên (SAB)
S, B là hình chiếu của chính nó trên (SAB)
\( \Rightarrow \) SB là hình chiếu của tam giác SBC trên (SAB)
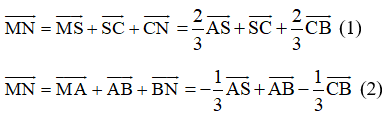
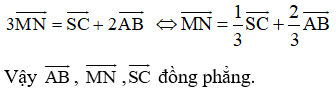
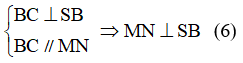
=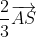 +
+ 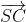 +
+ 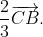 (1)
(1)
=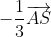 +
+  +
+ 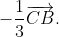 (2)
(2)
Nhân (2) với 2 rồi cộng với (1) ta được: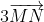 =
= 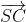 +
+ 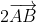
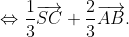
Vậy ,
, 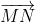 ,
, 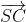 đồng phẳng.
đồng phẳng.
kiểu này là tự đăng rồi