Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC hay BMNC là hình thang

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
b: Xét ΔAED có AH/AE=AM/AD
nên HM//ED
=>ED//CB
Xet ΔCAE có
CH vừa là đường cao, vừa là trung tuyến
=>ΔCAE can tại C
=>CA=CE=BD
Vì BC//ED và BD=CE
nên BCDE là hình thang cân
c: Xét tứ giác AHCK có
N là trung điểm chung của AC và HK
góc AHC=90 độ
=>AHCK là hình chữ nhật

Lời giải chi tiết bài toán:
Đề bài:Cho tam giác ABCABC vuông tại AA, có AB=aAB = a. Gọi M,N,DM, N, D lần lượt là trung điểm của AB,BC,ACAB, BC, AC.
- Chứng minh NDND là đường trung bình của tam giác ABCABC và tính độ dài của NDND theo aa.
- Chứng minh tứ giác ADNMADNM là hình chữ nhật.
- Gọi QQ là điểm đối xứng của NN qua MM. Chứng minh AQBNAQBN là hình thoi.
- Trên tia đối của tia DBDB lấy điểm KK sao cho DK=DBDK = DB. Chứng minh 3 điểm Q,A,KQ, A, K thẳng hàng.
-
Vì NN là trung điểm của BCBC và DD là trung điểm của ACAC, theo định nghĩa đường trung bình:
NDND song song với ABAB và ND=12ABND = \frac{1}{2}AB. -
Do AB=aAB = a, suy ra ND=12aND = \frac{1}{2}a.
Kết luận: NDND là đường trung bình của tam giác ABCABC, và ND=12aND = \frac{1}{2}a.
2. Chứng minh tứ giác ADNMADNM là hình chữ nhật:-
MM là trung điểm của ABAB, nên AM=MB=12AB=12aAM = MB = \frac{1}{2}AB = \frac{1}{2}a.
-
ND∥ABND \parallel AB và ND=12ABND = \frac{1}{2}AB (tính chất đường trung bình).
-
AM⊥ABAM \perp AB (tam giác vuông tại AA), nên AM⊥NDAM \perp ND.
-
Tứ giác ADNMADNM có:
- AD∥MNAD \parallel MN (vì cùng vuông góc với ABAB).
- AM⊥NDAM \perp ND.
Do đó, ADNMADNM là hình chữ nhật.
3. Chứng minh AQBNAQBN là hình thoi:-
QQ là điểm đối xứng của NN qua MM, nên MQ=MNMQ = MN.
-
Vì MM là trung điểm của ABAB, suy ra AQ=BN=AB=aAQ = BN = AB = a.
-
Trong hình chữ nhật ADNMADNM:
- AM=ND=12aAM = ND = \frac{1}{2}a, và MM là trung điểm của ABAB.
-
Tứ giác AQBNAQBN có:
- AQ=BNAQ = BN.
- AB=QN=aAB = QN = a.
Vậy AQBNAQBN là hình thoi.
4. Chứng minh 3 điểm Q,A,KQ, A, K thẳng hàng:-
Trên tia đối của tia DBDB, lấy điểm KK sao cho DK=DBDK = DB.
-
QQ đối xứng với NN qua MM, nên MQ=MNMQ = MN.
-
Trong tam giác vuông ABCABC, DD và MM lần lượt là trung điểm của ACAC và ABAB:
- DB=AC2+AB22=a2+AC22DB = \frac{\sqrt{AC^2 + AB^2}}{2} = \frac{\sqrt{a^2 + AC^2}}{2}.
- DK=DBDK = DB, nên KK nằm trên đường thẳng qua DD kéo dài.
-
Vì AQBNAQBN là hình thoi, nên AQAQ song song với DBDB. Kết hợp với vị trí của KK, suy ra Q,A,KQ, A, K thẳng hàng.
- NDND là đường trung bình của tam giác ABCABC, ND=12aND = \frac{1}{2}a.
- ADNMADNM là hình chữ nhật.
- AQBNAQBN là hình thoi.
- Ba điểm Q,A,KQ, A, K thẳng hàng.

a: Xét tứ giác ABDC có
E là trung điểm của BC
E là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật

Lời giải:
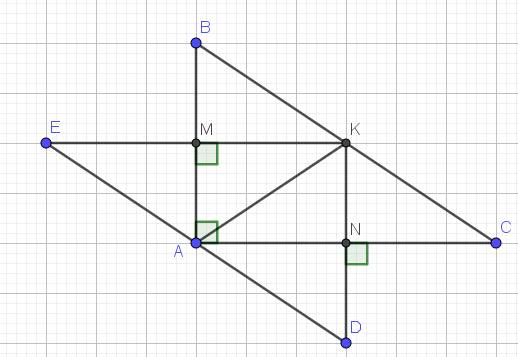
a. Tứ giác $AMKN$ có 3 góc vuông $\widehat{A}=\widehat{M}=\widehat{N}=90^0$ nên $AMKN$ là hình chữ nhật.
b.
Xét tam giác $AEM$ và $AKM$ có:
$MA$ chung
$\widehat{AME}=\widehat{AMK}=90^0$
$EM=KM$ (do $E,K$ đối xứng nhau qua $M$)
$\Rightarrow \triangle AEM=\triangle AKM$ (c.g.c)
$\Rightarrow \widehat{EAM}=\widehat{KAM}(1)$
Tương tự:
$\triangle AKN=\triangle ADN$ (c.g.c)
$\Rightarrow \widehat{DAN}=\widehat{KAN}(2)$
Từ $(1); (2)\Rightarrow \widehat{EAM}+\widehat{MAN}+\widehat{DAN}=\widehat{KAM}+\widehat{MAN}+\widehat{KAN}=2\widehat{MAN}=2.90^0=180^0$
Hay $\widehat{EAD}=180^0$
$\Rightarrow E, A, D$ thẳng hàng.