Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) BD, CE là các đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DA = DC; EA =EB
\(\Rightarrow\)ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)ED // BC; ED = 1/2 BC
\(\Delta GBC\)có MG = MB; NG = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta GBC\)
\(\Rightarrow\)MN // BC; MN = 1/2 BC
suy ra: MN // ED; MN = ED
\(\Rightarrow\)tứ giác MNDE là hình bình hành
c) MN = ED = 1/2 BC
\(\Rightarrow\)MN + ED = \(\frac{BC}{2}\)+ \(\frac{BC}{2}\)= BC
a) Vì BM là trung tuyến AC
=> M là trung điểm AC (1)
Vì CN là trung tuyến AB
=> N là trung tuyến AB (2)
Từ (1) và (2) => MN là đường trung bình ∆ABC
=> MN //BC , MN = \(\frac{1}{2}BC\)
Vì E là trung điểm GB
F là trung điểm GC
=> FE là đường trung bình ∆GBC
=> FE//BC
=> FE = \(\frac{1}{2}BC\)
=> NM //FE
=> FE= NM
=> NMFE là hình bình hành
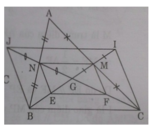
a) Ta có MN là đường trung bình của ΔABC
⇒ MN // BC và MN = BC/2
Tương tự EF là đường trung bình của ΔBGC nên EF // BC và EF = BC/2
Do đó MN // EF và MN = EF.
Vậy MNEF là hình bình hành (hai cạnh đối vừa song song vừa bằng nhau)
b) Ta có G là trong tâm của ΔABC nên GN = GC/2
Mà GN = JN (gt) ⇒ GJ = GC.
Tương tự ta có GI = GB
Vậy tứ giác BJIC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
TL:
a,G là trọng tâm của tam giác ABC nên GD =1/2 BG suy ra GM= GD
Tương tự EG=GN suy ra MNDE là hình bình hành
a) Trong tam giác ABC , có :
EA = EB ( CE là trung tuyến )
DA = DC ( DB là trung tuyến )
=> ED là đường trung bình của tam giác ABC
=> ED // BC (1) , DE = 1/2 BC (2)
Trong tam giác GBC , có :
MG = MB ( gt)
NG = NC ( gt)
=> MN là đương trung bình của tam giác GBC
=> MN // BC (3) , MN = 1/2 BC (4)
Từ 1 và 2 => ED // MN ( * )
Từ 3 và 4 => ED = MN ( **)
Từ * và ** => EDMN là hbh ( DHNB )
a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
hay BCMN là hình thang
A B C M N
GT/KL: Bn tự lm nhé
CM:
Xét tam giác ABC, ta có: AN =NB(gt) ; AM= MC(gt) => MN là đường trung bình của tam giác ABC
=> MN = \(\frac{1}{2}\)BC=6(cm); MN // BC (1)
b)Xét tam giác GBC,ta có: GE =EB (gt); GF=FC(gt)=> EF là đường trung bình của tam giác GBC
=> EF = \(\frac{1}{2}\)BC= 6(cm); EF // BC (2)
Từ (1) và (2) => EF // MN; EF =MN
⇒ AH là đường trung tuyến của ∆ABC
Ta có:
G là giao điểm của hai đường trung tuyến BM và CN của ∆ABC (gt)
Mà AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH đi qua G
Vậy A, G, H thẳng hàng.