Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
b: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
góc EAH=góc DAH
=>ΔAEH=ΔADH
=>AE=AD và HE=HD
=>AH là trung trực của DE

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB\cdot AF=AC\cdot AE\)(đpcm)
b)Sửa đề: \(\widehat{BAD}=\widehat{BED}\)
Xét tứ giác BDEA có
\(\widehat{BEA}=\widehat{BDA}\left(=90^0\right)\)
\(\widehat{BEA}\) và \(\widehat{BDA}\) là hai góc cùng nhìn cạnh BA
Do đó: BDEA là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay \(\widehat{BAD}=\widehat{BED}\)(hai góc cùng nhìn cạnh BD)

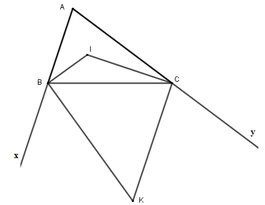
Ta có:
ICK=ICB+KCB
=1/2ACB+1/2BCx
=1/2 180=90
Hoàn toàn tương tự thì:IBK=90
Xét tứ giác BICK có:
CIB+IBC+ICB+CKB=360
=>CIB=360-(IBC+ICB+CKB)=360-235=125
Vậy các góc của tứ giác BICK là CIB=125, CKB=55
IBK=ICK=90
hình bạn tự vẽ nha !chúc bạn học tốt

a: Xét ΔAEB vuông tại E và ΔAFC vuôg tại F có
góc BAE chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
b: Xét tứ giác AFHE có
góc AFH+góc AEH=180 độ
=>AFHE nội tiếp
=>góc FAH=góc FEH
=>goc BAD=góc BEF

Ta có : KABˆ=KADˆKAB^=KAD^ ( AK là tia phân giác A^A^ )
Mà KABˆ=AKDˆKAB^=AKD^ ( so le trong )
\Rightarrow AKDˆ=KADˆAKD^=KAD^
\Rightarrow △△ ADK cân tại D
\Rightarrow AD = KD (1)
Lại có : KBAˆ=KBCˆKBA^=KBC^ ( BK là tia phân giác B^B^ )
Mà KBAˆ=BKCˆKBA^=BKC^ ( so le trong )
\Rightarrow KBCˆ=BKCˆKBC^=BKC^
\Rightarrow △△ BCK cân tại C
\Rightarrow BC = CK (2)
Cộng (1) và (2) có :
AD + BC = KD + CK
\Rightarrow AD+BCTổng hai cạnh bên=CDCạnh đáy

A B C D E F I
Vẽ ID,IE,IF lần lượt vuông góc với AB,BC,AC.Ta có :
I thuộc phân giác\(\widehat{ABC}\)nên ID = IE ; I thuộc phân giác\(\widehat{ACB}\)nên IE = IF => ID = IF
=> I thuộc phân giác\(\widehat{BAC}\)hay AI là phân giác\(\widehat{BAC}\)