Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tam giác abc.gọi k là 1 điểm thuộc đường phân giác của góc ngoài tại a. chứng minh ab+ac<kb+kc


a) Xét tam giác BAI vuông tại A và tam giác BKI vuông tại K có
. BH: cạnh chung
. ABH=KHI ( BI là tia phân giác của ABC)
Nên tam giác BAI= tam giác BKI ( ch-gn)
Nên ta có:
.AB=KB ( yếu tố tương ứng )
b) Xét tam giác ABH và tam giác KBN có
. BA=BK ( tam giác BAI=tam giác BKI )
. ABH=KBH ( gt)
BH: cạnh chung
Nên tam giác ABH= tam giác KBH (c-g-c)
Nên ta có:
BHA=BHK ( yếu tố tương ứng )
Mà BHA+BHK= 180 độ ( kề bù)
Nên BHA=BHK= 180độ:2 = 90 độ
Suy ra BI vuông góc với AK
c)Xét tam giác AMI vuông tại A và tam giác KCI vuông tại K có
. AI=KI (tam giác BAI= tam giác BKI )
. AIK=KIC ( đối đỉnh )
Nên tam giác AMI= tam giác KCI ( cgv-gnk)
Ta có:
BA=BK ( tam giác BAI= tam giác BKI)
AM=KC ( tam giác AIM=tam giác KIC)
Nên: BA+AM=BK+KC
Suy ra BM=BC
Xét tam giác MIC có
. MI=CI
Nên tam giác MIC cân tại I
Xét tam giác BMI và tam giác BCI có
. MI=IC ( tam giác AIM= tam giác KIC )
. BM=BC (cmt)
BI: cạnh chung
Nên tam giác BMI=tma giác BCI (c-c-c)
Ta có:
BMI=BCI (tam giác BMI= tam giác BCI )
Ta cũng có:
IME=ICE ( tam giác IMC cân tại I)
Nên BMI+IME=BCI+ICE
Suy ra BMC=BCM

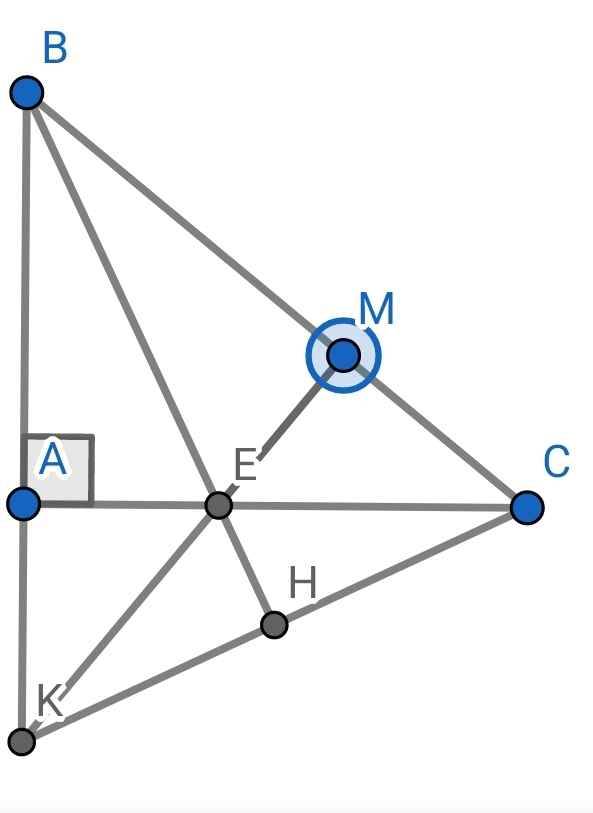
a) Xét ∆ABE và ∆MBE có:
BE chung
góc ABE = góc MBE (BE là phân giác của góc ABC)
AB = BM
⇒∆ABE = ∆MBE (c-g-c)
⇒góc BAE = góc BME (hai góc tương ứng)
⇒ME vuông góc BC
b) Do ∆ABE = ∆MBE (cmt)
⇒AE = ME (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AEK và ∆MEC có:
AE = ME (cmt)
góc AEK = góc MEC (đối đỉnh)
⇒∆AEK = ∆MEC (cạnh góc vuông - góc nhọn kề)
⇒EK = EC (hai cạnh tương ứng)
AK = MC (hai cạnh tương ứng)
Lại có: BK = BA + AK
BC = BM + MC
⇒BK = BC
c) Gọi H là giao điểm của BE và CK
Xét ∆BHK và ∆BHC có:
BK = BC (cmt)
góc HBK = góc HBC (do BE là tia phân giác của góc ABC)
BH chung
⇒∆BHK = ∆BHC (c-g-c)
⇒góc BHK = góc BHC (hai góc tương ứng)
Mà góc BHK + góc BHC = 180⁰ (kề bù)
⇒góc BHK = góc BHC = 180⁰ : 2 = 90⁰
⇒BH vuông góc KC
Hay BE vuông góc KC

Bài 1: ...., tia phân giác BE của ABC ( E thuộc AC)...
như z pải ko bn
a) Xét tam giác ABE vuông tại A và tam giác FBE vuông tại F
có: BE là cạnh chung
góc ABE = góc FBE ( gt)
=> tam giác ABE = tam giác FBE ( cạnh huyền- góc nhọn)
=> AE = FE ( 2 cạnh tương ứng) (1)
Xét tam giác AEK vuông tại A và tam giác FEC vuông tại F
có: AE = FE(cmt)
góc AEK = góc FEC ( đối đỉnh)
=> tam giác AEK = tam giác FEC ( cạnh góc vuông- góc nhọn)
=> EK = EC ( 2 cạnh tương ứng)
Xét tam giác FEC vuông tại F
có: FE < EC ( quan hệ cạnh huyền và cạnh góc vuông) (2)
Từ(1);(2) => AE< EC
b) ta có: tam giác ABE = tam giác FBE ( chứng minh phần a)
=> AB = FB ( 2 cạnh tương ứng) (1)
ta có: tam giác AEK = tam giác FEC ( chứng minh phần a)
=> AK = FC ( 2 cạnh tương ứng) (2)
Từ (1);(2) => AB+ AK = FB+ FC
=> BK = BC
=> tam giác BKC cân tại B ( định lí)
mà BE là tia phân giác của góc KBC
=> BE là đường trung trực của KC ( định lí)
c) Xét tam giác ABC vuông tại A
có: góc ABC + góc C = 90 độ ( 2 góc phụ nhau)
thay số: 70 độ + góc C = 90 độ
góc C = 90 độ - 70 độ
góc C = 20 độ
ta có: góc FBE = góc ABC/2 = 70 độ/2 = 35 độ ( tính chất tia phân giác)
=> góc FBE = 35 độ
Xét tam giác BEC
có: góc C + góc FBE + góc BEC = 180 độ ( định lí tổng 3 góc trong tam giác)
thay số: 20 độ + 35 độ + góc BEC = 180 độ
góc BEC =180 độ - 20 độ - 35 độ
góc BEC = 125 độ
Học tốt nhé bn !!!!
xin lỗi bn nha! nhưng mk ko bít kẻ hình

a: Xét ΔAHC vuông tại H và ΔKHC vuông tại H có
HA=HK
HC chung
Do đó: ΔAHC=ΔKHC
b: Xét ΔEBD và ΔECA có
EB=EC
\(\widehat{BED}=\widehat{CEA}\)(hai góc đối đỉnh)
ED=EA
Do đó: ΔEBD=ΔECA
=>\(\widehat{EBD}=\widehat{ECA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//AC
c: Xét ΔEAH vuông tại H và ΔEKH vuông tại H có
AH=KH
EH chung
Do đó: ΔEAH=ΔEKH
=>\(\widehat{AEH}=\widehat{KEH}\)
=>EB là phân giác của góc AEK