Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Em tự giải
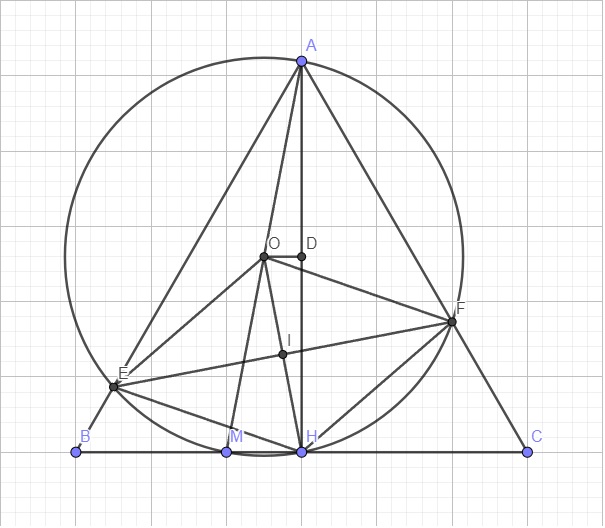
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H

Xin lỗi bạn nha ! Vì lỗi nên mình không vẽ được hình cho bạn ,có j bạn tự vẽ nha !!!
Bài giải
a) AB là tiếp tuyến tại A của ( C)
=> \(\widehat{BAF}=\widehat{AEF}\)
Xét \(\Delta ABF\)và \(\Delta EBA\)có :
\(\hept{\begin{cases}\widehat{ABE}chung\\\widehat{BAF}=\widehat{BEA}\end{cases}\Rightarrow\Delta ABF}\infty\Delta EBA\left(g-g\right)\)
\(\Rightarrow\frac{AB}{BE}=\frac{BF}{AB}\Rightarrow AB^2=BE.BF\)
Xét \(\Delta ABC\) vuông tại A có đường cao AH .
=> AB2 =BH . BC
=> BH . BC = BE . BF ( =AB2 )
Xét \(\Delta BHF\)và \(\Delta BEC\)có :
\(\frac{BH}{BE}=\frac{BF}{BC}\)
\(\widehat{CBE}\)chung
=> \(\Delta BHF\infty\Delta BEC\left(c-g-c\right)\)
=> \(\widehat{BHF}=\widehat{BEC}\)
*) \(\widehat{BHF}+\widehat{FHC}=\widehat{BEC}+\widehat{FHC}\)
\(\Leftrightarrow\widehat{FEC}+\widehat{FHC}=\widehat{BHC}=180^O\)
=> EFHC là tứ giác nội tiếp ( có tổng 2 góc đối =180 o
b) EFHC là tứ giác nội tiếp
=> \(\widehat{EHC}=\widehat{EFC}\)( cùng chắn góc EC )
\(\widehat{FEC}=\widehat{BHF}\)( c/ m cân A )
Mà \(\widehat{FEC}=\widehat{EFC}\)( \(\Delta ECF\)cân ở C )
=> \(\widehat{EHC}=\widehat{BHF}\)
=> 90O \(-\widehat{EHC}=90^O-\widehat{BHF}\)
<=> \(\widehat{EHD}=\widehat{FHD}\)
=> HD là phân giác góc EHF

b/ Gọi G là giao điểm của AB và DF
Ta có :
Góc ACQ = góc AHQ ( t/g ACHQ n.t )
Góc ACQ = góc ADF ( 2 góc n.t chắn cung AF )
=> Góc AHQ = góc ADF
Mà 2 góc ở vị trí đồng vị
Nên \(HQ//DF\)
Mặc khác \(HQ\perp AB\)tại Q
=> \(DF\perp AB\)tại G
Xét tứ giác GBNF ta có:\(B\widehat{G}F+B\widehat{N}F=180^0\)
=> Tứ giác GBNF nội tiếp =>\(N\widehat{G}F=N\widehat{B}F\)
Mà \(N\widehat{B}F=C\widehat{A}F\)( tứ giác ACBF n.t (O))
Nên \(N\widehat{G}F=C\widehat{A}F\left(1\right)\)
Xét tứ giác GMAF ta có: \(A\widehat{M}F=A\widehat{G}F\left(=90^0\right)\)
=> Tứ giác GMAF n.t =>\(M\widehat{A}F+M\widehat{G}F=180^0\left(2\right)\)
(1) và (2) => \(N\widehat{G}F+M\widehat{G}F=180^0\)
=> \(\overline{M,G,N}\)
Mà G là giao điểm của AB và DF
Nên MN,AB,DF đồng quy tại G
MN là đường thẳng simson nha bạn


Ta có: MP vuông góc AB (gt)
=) Góc MPA = 90độ (1)
Lại có: MQ vuông góc AC (gt)
=) Góc MQA = 90 độ (2)
Từ (1) và (2) =) góc MPA + góc MQA = 180độ
Mà 2 góc ở vị trí đối nhau
=) Tứ giác APMQ nội tiếp