Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tam giác ABC , có AB=AC . Lấy M là trung điểm của BC . a) chúng minh tam giác ABM = tam giác ACM và tia AM là tia phân giác của góc BAC . b) lấy điểm D thuộc tia đối của tia BC và điểm E thuộc tia đối của tia CCB sao cho BD = CE. Kẻ BH vuông góc với AD tại H, kẻ CI vuông góc với AE tại I. Chứng minh : tam giác ABH = tam giác ACE , DH = EI. c) trong trường hợp BH = BA và góc BAC = 90 độ, tính BDA
#Hỏi cộng đồng OLM
#Toán lớp 7

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Suy ra: AM là tia phân giác của góc BAC

a) Xét tam giác AMB và tam giác AMC ta có:
AM chung
AB=AC (gt)
MB=MC (vì M là trung điểm của BC)
Suy ra tam giác AMB=tam giác AMC (c-c-c) (đpcm)
b) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc BAM=góc CAM (2 góc tương ứng)
Suy ra AM là tia phân giác của góc BAC (đpcm)
c) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc AMB=góc AMC(2 góc tương ứng)
Mà góc AMB+góc AMC=180 độ (2 góc kề bù)
Suy ra góc AMB=góc AMC=180 độ/2=90 độ
Suy ra AM vuông góc với BC tại M (đpcm)
Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc ACM=góc ABM (2 góc tương ứng) (đpcm)

a) Mk cm trường hợp = nhau c.c.c nhé ! trường hợp c.g.c cũng có thể làm đó bn
Do tam giác ABC cân tại A => AB=AC
\(\widehat{B}=\widehat{C}\)
Do AM là đường trung tuyến ứng vs cạnh BC => BM=CM
Xét tam giác ABM và tam giác ACM có :
AB = AC ( cm trên )
AM là cạnh chung
BM=CM ( cm trên )
nên tam giác ABM = tam giác ACM
b) Do tam giác ABC cân tại A và có AM là đường trung tuyến => AM cũng là đường trung trực của tam giác ABC ( theo t/c tam giác cân )
( hoặc bn cũng có thể cm cách khác nhưng dài hơn , cách này ngắn nhất đó ! )
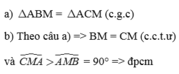
a) Xét tam giác ABM và tam giác ACM:
+ AM chung.
+ AB = AC (gt).
+ \(\widehat{ABM}=\widehat{ACM}\) (AM là phân giác \(\widehat{BAC}\) ).
\(\Rightarrow\) Tam giác ABM = Tam giác ACM (c - g - c).
b) Xét tam giác ABC: AB = AC (gt).
\(\Rightarrow\) Tam giác ABC cân tại A.
Mà AM là phân giác \(\widehat{BAC}\) (gt).
\(\Rightarrow\) AM là trung tuyến (Tính chất tam giác cân).
\(\Rightarrow\) M là trung điểm của BC.