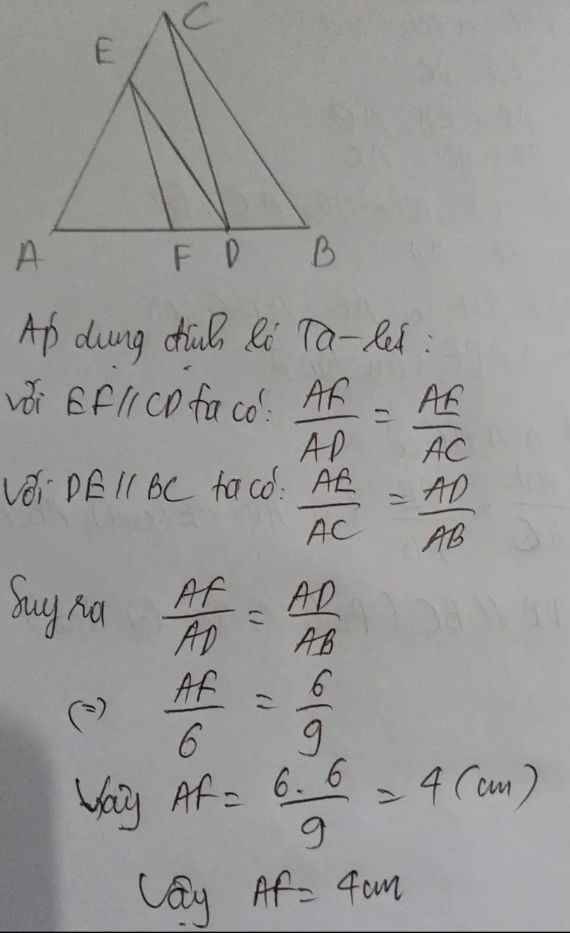Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ơi bạn kiểm tra lại xem có nhầm chỗ nào không vì:
Nếu EF //AD mà F,D nằm trên AB thì EF và AD có điểm F chung nên không thể //.

Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C

Đáp án đúng là: A
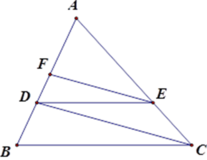
Áp dụng định lí Thalès:
• Với DE // BC (E ∈ AC) ta có: \(\dfrac{{A{\rm{D}}}}{{AB}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{6}{{9}} = \dfrac{2}{3}\)
• Với EF // CD (F ∈ AB) ta có: \(\dfrac{{AF}}{{A{\rm{D}}}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{2}{3}\)
Suy ra: \({\rm{AF}} = \dfrac{2}{3}A{\rm{D}} = \dfrac{2}{3}.6 = 4(cm)\)
Vậy AF = 4 cm.

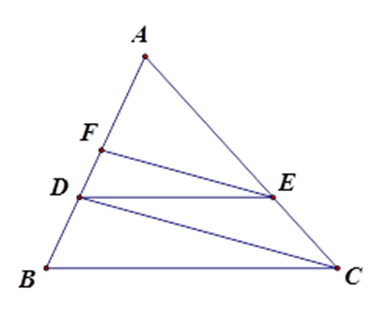
Áp dụng định lí Ta-lét:
+với EF//CD ta có \(\frac{AF}{AD}=\frac{AE}{AC}\)
+với DE//BC tác có \(\frac{AE}{AC}=\frac{AD}{AB}\)
suy ra \(\frac{AF}{AD}=\frac{AD}{AB}\),
tức là \(\frac{AF}{6}\)\(=\frac{6}{9}\)
=> AF=\(\frac{6.6}{9}=4\left(cm\right)\)
CHÚC BẠN HỌC TỐT

a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc A chung
=>ΔABC đồng dạng vơi ΔAED
b: EF//AB
=>EF/AB=CE/CA
=>EF/18=5/8
=>EF=90/8=11,25(cm)
BF/FC=AE/EC=3/5

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6