Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

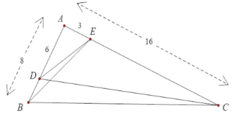
c) Ta có AE=AC-EC(vì E thuộc AC)
mà AC=16, EC=13(gt)
=>AE=16-13=3(cm)
Ta có: AD=AB-BD(D thuộc AB)
mà AB=8, BD=2(gt)
=>AD=8-2=6(cm)
Có: AE.AC=3.16=48
AD.AB=6.8=48
a+b)Có AE.AC=AD.AB(cmt)
=>AE/AB=AD?AC(tính chất tỉ lệ thức)
Xét tam giác AED và tam giác ABC có: góc A chung
AE/AB=AD/AC(cmt)
=>tam giác AED đồng dạng tam giác ABC(cgc)
=>góc AED=góc B(2 góc tương ứng)

a) Ta có: AB-DB=AD=> AD=8-2=6cm
AC-EC=AE=16cm-13cm=AE=>AE=3cm
Xét △AEB và △ADC có góc A chung
AE:AD=3:6=1:2
AB:AC=8:16=1:2
=>AE:AD=AB:AC=1:2
=>△AEB đồng dạng với △ADC
b) Ta có: AE/AD=AB/AC(cmt)=>AE/AB=AD/AC
Xét △AED và △ABC có:
EAD=BAC
AE/AB=AD/AC
=> AED=ABC .

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
Ta có: \(\hat{BAD}+\hat{CAD}=\hat{BAC}=90^0\)
\(\hat{BDA}+\hat{HAD}=90^0\) (ΔHAD vuông tại H)
mà \(\hat{BAD}=\hat{BDA}\) (ΔBAD cân tại B)
nên \(\hat{CAD}=\hat{HAD}\)
=>AD là phân giác của góc HAC
b: Xét ΔAHD và ΔAED có
AH=AE
\(\hat{HAD}=\hat{EAD}\)
AD chung
Do đó: ΔAHD=ΔAED
=>\(\hat{AHD}=\hat{AED}\)
=>\(\hat{AED}=90^0\)
=>ED⊥AC
mà HK⊥AC
nên HK//ED
=>HKED là hình thang
c: ΔAHD=ΔAED
=>DH=DE
=>D nằm trên đường trung trực của HE(1)
Ta có: AH=AE
=>A nằm trên đường trung trực của HE(2)
Từ (1),(2) suy ra AD là đường trung trực của HE
=>AD⊥HE
Xét ΔAEH có
HK,AD là các đường cao
HK cắt AD tại I
Do đó: I là trực tâm của ΔAEH
=>EI⊥AH tại F
mà HC⊥HA
nên EF//HC
=>EFHC là hình thang
Hình thang EFHC có EF⊥FH
nên EFHC là hình thang vuông

Ta có:
A E A B = 3 8 ; A D A C = 6 16 = 3 8 ⇒ A E A B = A D A C
Xét ΔAED và ΔABC có A chung và A E A B = A D A C (cmt)
Nên ΔAED ~ ΔABC (c.g.c)
Đáp án: C

a) Ta có: AD=AB-DB=8cm-2cm
⇒AD=6cm
AE=AC-EC=16cm-3cm
⇒AE=3cm
Xét △AEB và △ADC ta có:
góc A chung
AE/AD=3/6=1/2
AB/AC=8/16=1/2
⇒AE/AD=AB/AC=1/2
⇒△AEB đồng dạng với △ADC
+ Xét ΔABE và ΔACD có A chung và A E A D = A B A C ( = 1 2 ) nên
ΔABE ~ ΔACD (c - g - c) suy ra góc A B E ^ = A C D ^ (hai góc tương ứng) và => AE.CD = AD.BE
+ ΔAED ~ ΔABC (cmt) nên A E A B = A D A C ⇔ AE.AC = AB.AD
Nên A, C, D đúng, B sai.
Đáp án: B