Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này nếu sử dụng định lý Talet ở HK 2 lớp 8 sẽ nhanh. Bạn có thể dùng cách ở HKI như sau:
Hình vẽ hơi xấu xíu nhe :))
A B C M N 1 1
a) Tam giác ABC cân suy góc B1=90-(A/2)
Ta có: AM=AB-BM=AC-CN=AN
suy ra t/g AMN cân, đỉnh A
suy ra góc M1= 90-(A:2)
Do đó góc M1= B1
suy ra MN//BC
Tứ giác BCNM có MN//BC và BM=CN(gt) nên là hình thang cân.
b) theo câu a) B1=90-(A:2)=90-(40:2)=70
ABC=B1=70 độ
BMN= 180-70=110 độ (hai góc trong cùng phía bù nhau)
CNM=110 độ
c) Nếu BM=MN thì tg MBN cân
suy ra góc MBN= góc MNB
mà MNB=CBN(so le trong)
Do đó góc MBN= góc CBN
suy ra BN là phân giác của góc B.
Tương tự, CM là phân giác của góc C
Vậy khi BM=MN=CN thì M và N sẽ lần lượt là giao điểm của tia phân giác góc B và C ứng với cạnh AB và AC

A 40độ N M 1 2 1 2 1 1 C B
\(\hept{\begin{cases}AB=AC\\BM=CN\end{cases}}\Rightarrow AN=AM\)
\(\Rightarrow\frac{AM}{AB}=\frac{A}{AC}\)
\(\Rightarrow MN//BC\text{ mà }NC=BM\)
=> MNCB là hình thang cân
A B C M N
Ta có: \(\Delta ABC\) cân tại A => AB = AC
Mà BM = CN (gt)
=> AB - MB = AC - CN
=> AM = AN
=> M là trung điểm của AB (1)
N là trung điểm của AC (2)
Trong tam giác ABC có (1) và (2)
=> MN là đường trung bình của tam giác ABC
=> MN // BC
=> BMNC là hình thang

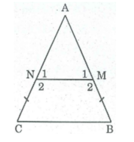
∆ ABC cân tại A
⇒ ∠ B = ∠ C = ( 180 0 - ∠ A) / 2 (tính chất tam giác cân) (1)
AB = AC (gt) ⇒ AM + BM = AN + CN
Mà BM = CN (gt) ⇒ AM = AN
⇒ ∆ AMN cân tại A
⇒ ∠ M 1 = ∠ N 1 = ( 180 0 - ∠ A) / 2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠ M 1 = ∠ B
⇒ MN // BC (vì có cặp góc đồng vị bằng nhau)
Tứ giác BCNM là hình thang có ∠ B = ∠ C
Vậy BCNM là hình thang cân.

a) Chứng minh BN là tia phân giác của góc N, CN là tia phân giác của góc C nên điểm M;N là đường phân giác của hình tam giác ABC
thì BM = MN = NC.

Bài giải
a/ Tứ giác BMNC là hình thang cân do có hai góc ở đáy bằng nhau(tam giác ABC cân tại A)
b/ Ta có : Góc A+ góc B + góc C=180o (tổng các góc trong tam giác)
(góc B + góc C)=180o - góc A=180o -40o =140o
Mà góc B = Góc C ( tam giác ABC cân )
Suy ra góc B=Góc C=140o :2=70o
Ta lại có: Hình thang BMNC cân BMNC có:
góc MNC=góc NMB(2 góc kề một đáy bằng nhau)
Mà góc B+góc C +góc MNC+góc NMB=360o ( tổng các góc trong tứ giác )
suy ra góc MNC+góc NMB=360o -(góc B + góc C)=360o -140o =220o
Mà góc MNC= góc NMB
suy ra góc MNC=góc NMB=220o :2=110o
o0 học tốt nhé 0o

Cậu có nhầm đề không vậy ??? Nếu vẽ như đề cậu thì chắc chắn cái tứ giác đó cũng chỉ là tứ giác bình thường thôi

câu a mình chắc chắn bạn biết trả lời còn câu b thì chứng minh BN là tia phân giác của góc N, CN là tia phân giác của góc C nên các điểm M, N là đường phân giác của tam giác ABC thì BM=MN=NC vậy thôi nhé