Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: O nằm trên đường trung trực của AB
=>OA=OB(1)
O nằm trên đường trung trực của AC
=>OA=OC(2)
từ (1),(2) suy ra OB=OC
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\hat{ABO}=\hat{ACO}\)
Xét ΔOBD và ΔOCE có
OB=OC
\(\hat{OBD}=\hat{OCE}\overline{}\)
BD=CE
Do đó: ΔOBD=ΔOCE
b: ΔOBD=ΔOCE
=>OD=OE
=>O nằm trên đường trung trực của DE(3)
ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
=>A nằm trên đường trung trực của DE(4)
Từ (3),(4) suy ra AO là đường trung trực của DE
c: Xét ΔABC có \(\frac{AD}{DB}=\frac{AE}{EC}\)
nên DE//BC
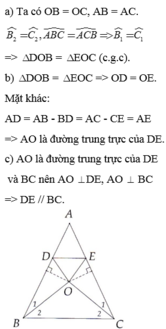
a)
\(O\) cách đều \(B\) và \(C\) ⇒ \(O B = O C\)
Giả thiết: \(B D = C E\)
Góc \(\angle D B O = \angle E C O\) do tam giác \(A B C\) cân, \(A O\) là trục đối xứng.
⇒ \(\triangle D O B = \triangle E O C\) (c.g.c).
b)
Từ (a) suy ra \(O D = O E\) ⇒ \(A O\) qua trung điểm \(D E\)
\(A O\) vuông góc \(D E\) (vì là trục đối xứng)
\(A O\) là đường trung trực của \(D E\).
c)
\(A O \bot B C\) và \(A O \bot D E\)
Hai đường cùng vuông góc với \(A O\) ⇒ DE\\BC
nhé bạn cảm ơn bí ẩn đã nhắc nhở\(\)

Tự vẽ hình
a, Do tam giác ABC cân tại A ( gt )
=> AB = AC ; ABC = ACB ( tính chất tam giác cân)
Xét tam giác ABD và tam giác ACE có :
Góc BAC chung
AB = AC ( cmt )
ADB = AEC ( = 90 độ )
=> Tam giác ABD = ACE ( cạnh huyền - góc nhọn )
=> ABD = ACE ( 2 góc tương ứng )
AD = AE ( 2 cạnh tương ứng )
=> Tam giác ADE cân tại A ( định nghĩa tam giác cân )
=> ADE = AED ( tính chất tam giác cân )
Trong tam giác ABC có : ABC + ACB + BAC = 180 độ ( Tổng 3 góc của 1 tam giác )
Trong tam giác AED có : AED + ADE + BAC = 180 độ ( tổng 3 góc của 1 tam giác )
=> ABC + ACB = AED + ADE
Mà ABC = ACB ; AED = ADE ( cmt )
=> 2.ABC = 2.AED => ABC = AED
Mà 2 góc này ở vị trí đồng vị => DE // BC ( Dấu hiệu nhận biết 2 đường thẳng song song )
Vậy DE // BC
b, Ta có : AE + BE = AB
AD + CD = AC
Mà AE = AD ; AB = AC ( cmt ) => BE = CD
Xét tam giác EOB và tam giác DOC có :
BDC = CEB ( = 90 độ )
BE = CD ( cmt )
ABD = ACE ( cmt )
=> tam giác EOB = DOC ( g.c.g )
=> OE = OD ( 2 cạnh tương ứng )
Vậy tam giác EOB = DOC
c, Ta có : AE = AD ( cmt ) => A nằm trên đường trung trực của đoạn thẳng DE
OE = OD ( cmt ) => O nằm trên đường trung trực của đoạn thẳng DE
=> AO là trung trực của đoạn thẳng DE
Vậy AO là trung trực của đoạn thẳng DE
d, Vì AO là trung trực của đoạn thẳng DE ( cmt )
=> AO // DE ( t/c đường trung trực )
Mà DE // BC ( cmt ) => AO vuông góc với BC ( từ vuông góc đến song song )
Xét tam giác ABC cân tại A có AH là đường trung tuyến
=> AH đồng thời là đường cao ứng với cạnh BC ( t/c tam giác cân )
=> AH vuông góc với BC
=> AH và AO trùng nhau => A,H,O thẳng hàng ( đpcm )

giúp mình với nhé mai mình thi cuối học kì I môn toán rồi. Chúc các bạn có một kì thi tốt đẹp.
đề bài sai à
câu a tam giác vuông tại A mà góc B = 90o suy ra góc C = 0o à

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

Tham khảo
Câu hỏi của Hot girl 2k5 - Toán lớp 7 - Học toán với OnlineMath
mik ko hieu cau c cho lam, ai giang giup mik cau c voi :((

a )
ta có : \(\widehat{C_1}=\widehat{C_2}\) ( 2 góc đối đỉnh )
mà \(\widehat{C_1}=\widehat{B}\) ( tam gíac ABC cân tại A )
Do do : \(\widehat{C_2}=\widehat{B}\)
xét \(\Delta ABDva\Delta ICE,co:\)
AB = AC = IC ( gt )
BD=CE ( gt )
\(\widehat{C_2}=\widehat{B}\) (cmt )
Do do : \(\Delta ABD=\Delta ICE\left(c-g-c\right)\)