Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình không biết vẽ hình khi trả lời nên bạn tự vẽ nhé
Đầu tiên chứng minh \(NE=\frac{1}{6}AN\)
Qua E kẻ đường thẳng song song BF cắt AC tại K
Theo ta-lét ta có:
\(\frac{FK}{FC}=\frac{BE}{BC}=\frac{1}{3}\)=>\(\frac{FK}{ÀF}=\frac{1}{6}=\frac{NE}{AN}\)
Từ E,N,C kẻ các đường cao tới AB lần lượt là H,G,I
Theo talet ta có
\(\frac{EH}{CI}=\frac{BE}{BC}=\frac{1}{3},\frac{NG}{EH}=\frac{AN}{AE}=\frac{6}{7}\)
=> \(\frac{NG}{CI}=\frac{2}{7}\)=> \(\frac{NG.AB}{CI.AB}=\frac{2}{7}\)
=> \(\frac{S_{ABN}}{S_{ABC}}=\frac{2}{7}\)
Tương tự \(\frac{S_{BPC}}{S_{ABC}}=\frac{2}{7}\),\(\frac{S_{AMC}}{S_{ABC}}=\frac{2}{7}\)
=> \(S_{MNP}=S_{ABC}-S_{AMC}-S_{ABN}-S_{BCP}=\frac{1}{7}S_{ABC}\)
Vậy \(S_{MNP}=\frac{1}{7}S_{ABC}\)

Câu hỏi của Bảo Châu Trần - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại đây nhé.
Bài 5:
Cho ABC vuông tại A, kẻ phân giác BM ( M AC), trên cạnh BC
lấy điểm E sao cho BE = AB
a) Chứng minh 2 tam giác BAM BEM .
b) Gọi F là giao điểm của đường thẳng ME và đường thẳng AB.
Chứng minh: FM = MC.
c) Chứng minh: AM < MC
d) Chứng minh AE // FC.


a) Ta thấy ngay \(\Delta ABE=\Delta ACD\) (Hai cạnh góc vuông)
b) Do \(\Delta ABE=\Delta ACD\Rightarrow\widehat{ABE}=\widehat{ACD}\)
mà \(\widehat{ABE}=\widehat{MAC}\) (Cùng phụ với góc BEA)
\(\Rightarrow\widehat{MAC}=\widehat{MCA}\) hay tam giác MAC cân tại M.
c) Xét tam giác vuông ADC: \(\widehat{MCA}=\widehat{MAC}\Rightarrow\widehat{MDA}=\widehat{MAD}\Rightarrow MD=MA\)
Vậy thì DM = MA = MC hay M là trung điểm DC.
Xét tam giácAIC có M là trung điểm DC, MK // DI nên MK là đường trung bình tam giác DIC.
Suy ra K là trung điểm IC.
d) Xét tam giác DIC có IM và DK là hai trung tuyến nên G là trọng tâm tam giác.
Gọi N là giao điểm của CG với DE thì DN = NI.
Áp dụng định lý Talet ta có:
\(\frac{MF}{DN}=\frac{CF}{CN}=\frac{FK}{NI}\)
Mà DN = NI nên MF = FK.

Gọi I trung điểm LE. Ta có DL//EN//OB và DL = EN = 0.5OB Þ DENL là hình bình hành. Tương tự chứng minh LMEF là hình bình hành. Từ đó suy ra EL,FM, DN đồng quy tại I
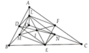

A B C D E F Q R I P
Ta có: \(S_{PQR}=S_{CFP}\Rightarrow S_{PQR}+S_{QPC}=S_{CFP}+S_{QPC}\Rightarrow S_{QRC}=S_{QFC}\)(Tính chất diện tích miền đa giác)
Ta thấy: \(\Delta QRC\)và \(\Delta QFC\)có chung đáy QC mà chúng có diện tích bằng nhau.
Nên chiều cao hạ từ R & F của 2 tam giác này bằng nhau => Khoảng cách từ 2 điểm R & F đến QC bằng nhau
Hay RF // QC => Tứ giác QRFC là hình thang.
Xét hình thang QRFC: FQ giao CR tại P; QR giao CF tại A.
Theo Bổ đề Hình thang (Search Mạng) thì AP đi qua trung điểm của đáy CQ (điểm I) => QI=CI
Xét \(\Delta AQI\)và \(\Delta ACI\)có: QI=CI (cmt); chung chiều cao hạ từ A xuống 2 đáy QI; CI
\(\Rightarrow S_{AQI}=S_{ACI}\). Tương tự: \(S_{PQI}=S_{PCI}\)\(\Rightarrow S_{AQI}-S_{PQI}=S_{ACI}-S_{PCI}\Rightarrow S_{APQ}=S_{APC}\)
Hay \(S_{ARP}+S_{PQR}=S_{AFP}+S_{CFP}\). Mà \(S_{PQR}=S_{CFP}\Rightarrow S_{ARP}=S_{AFP}\)
Lại có: \(S_{ADR}=S_{CFP}\Rightarrow S_{ARP}+S_{ADR}=S_{AFP}+S_{CFP}\Rightarrow S_{APD}=S_{APC}\)
Do 2 tam giác APD và APC chung chiều cao hạ từ A xuống 2 đáy PD & PC và có S bằng nhau
Nên PD=PC. Xét \(\Delta BPD\)và \(\Delta BPC\): PD=PC, chung chiều cao hạ từ B xuống PD và PC
\(S_{BPD}=S_{BPC}\Rightarrow S_{BDRQ}+S_{PQR}=S_{CEQP}+S_{BEQ}\). Mà \(S_{PQR}=S_{BEQ}\Rightarrow S_{BDRQ}=S_{CEQP}\)
Hoàn toàn tương tự: \(S_{CEQP}=S_{AFPR}\). Từ đó ta có: \(S_{AFPR}=S_{BDRQ}=S_{CEQP}\)(đpcm).
\(S_{DEF}=S_{BDF}+S_{DCE}+S_{AFE}+S_{ABC}=2\left(S_{ABD}+S_{BCE}+S_{AFC}\right)+S_{ABC}=2.\left(S_{ABC}+S_{ABC}+S_{ABC}\right)+S_{ABC}=7.S_{ABC}\)