Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy
a) đúng.
b) Đúng.
a) Ta có, theo quy tắc ba điểm của phép trừ:
=
–
(1)
Mặt khác, =
(2)
Từ (1) và (2) suy ra:
=
–
.
b) Ta có : =
–
(1)
=
(2)
Từ (1) và (2) cho ta:
=
–
.
c) Ta có :
–
=
(1)
–
=
(2)
=
(3)
Từ (1), (2), (3) suy ra đpcm.
d) –
+
= (
–
) +
=
+
=
+
( vì
=
) =
a) cos(;
) =
= 0
=> (;
) = 900
b) cos(;
) =
=
=> (;
) = 450
c) cos(;
) =
=
=> (;
) = 1500
Ta có +
=
=
= a
Ta có: –
=
+
.
Trên tia CB, ta dựng =
=> –
=
+
=
Tam giác EAC vuông tại A và có : AC = a, CE = 2a , suy ra AE = a√3
Vậy =
= a√3
Ta có cos(,
) = cos1350 =
sin(,
) = sin900 = 1
cos(,
) = cos00 = 1
Trước hết ta có
= 3
=>
= 3 (
+
)
=> = 3
+ 3
=> – = 3
=> =
mà =
–
nên
=
(
–
)
Theo quy tắc 3 điểm, ta có
=
+
=>
=
+
–
=> = –
+
hay
= –
+
Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có =
=>
=
= –
= –
= –
Theo quy tắc 3 điểm đối với tổng vec tơ:
=
+
=>
=
–
=
(
–
).
AK là trung tuyến thuộc cạnh BC nên
+
= 2
=>
–
+
= 2
Từ đây ta có =
+
=>
= –
–
.
BM là trung tuyến thuộc đỉnh B nên
+
= 2
=> –
+
= 2
=> =
+
.
a) Nối BM
Ta có AM= AB.cosMAB
=> || = |
|.cos(
,
)
Ta có: .
= |
|.|
| ( vì hai vectơ
,
cùng phương)
=> .
= |
|.|
|.cosAMB.
nhưng ||.|
|.cos(
,
) =
.
Vậy .
=
.
Với .
=
.
lý luận tương tự.
b) .
=
.
.
=
.
=> .
+
.
=
(
+
)
=> .
+
.
=
= 4R2
a) Ta có = 2
= 2
+ 0
suy ra
= (2;0)
b) = (0; -3)
c) = (3; -4)
d) = (0,2; – √ 3)
Từ định lí cosin a2 = b2 + c2 – 2bc. cosA
ta suy ra cos A =
= 
=> cosA ≈ 0,8089 =>
= 360
Tương tự, ta tính được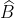
≈ 1060 28’ ; 
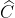≈ 370 32’.