Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

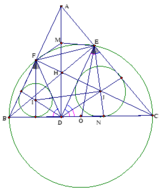
A B C D I R H K J M N O
Gọi M, N lần lượt là chân đường cao hạ từ B,C xuống AC,AB
Ta có \(DH.DA=DB.DC\)(1)
Để chứng minh K là trực tâm tam giác IBC ta chứng minh \(DK.DJ=DB.DC\)hay \(DK.DJ=DH.DA\)
Ta có NC,NA lần lượt là phân giác trong và phân giác ngoài của \(\widehat{MND}\)nên
\(\frac{HK}{HD}=\frac{NK}{ND}=\frac{AK}{AH}\)
\(\Rightarrow AK.HD=AD.HK\)
\(\Leftrightarrow HD\left(AD-DK\right)=AD\left(DK-DH\right)\)
\(\Leftrightarrow2.AD.DH=DK\left(DA+DH\right)\)
\(\Leftrightarrow2.AD.DH=2.DK.DJ\)
\(\Rightarrow AD.DH=DK.DJ\left(2\right)\)
Từ (1) và (2) ta có\(DK.DJ=DH.DA\)
=> K là trực tâm của tam giác IBC

Hình hơi rối, bạn tự vẽ hình nhé!
Lấy điểm S đối xứng với H qua BC, R là giao điểm của KC và MB.
Vì \(ME=MA=MH\)( tính chất trung tuyến )
Kết hợp tính đối xứng của điểm S ta có:
\(\widehat{MSB}=\widehat{BHD}=\widehat{MHE}=\widehat{MEB}\)
=> Tứ giác MESB nội tiếp
\(\Rightarrow\widehat{RBE}=\widehat{MSE}\left(1\right)\)
Lại có: \(\widehat{KSC}=\widehat{CHD}=\widehat{AHF}=\widehat{AEK}\)
Nên tứ giác KSCE cũng nội tiếp
=> \(\widehat{MSE}=\widehat{RCE}\left(2\right)\)
Từ ( 1 ) và ( 2 ) =>\(\widehat{RBE}=\widehat{RCE}\)
Nên tứ giác RBCE nội tiếp
=> \(\widehat{BRC}=\widehat{BEC}=90^o\)
Trong \(\Delta MBC\)có: \(MK\perp BC\)và \(CK\perp MB\)
Nên K là trực tâm của \(\Delta BMC\)

3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
Tứ giác BFEC có B E C ^ = B F C ^ = 90 0
=> tứ giác BFEC nội tiếp đường tròn đường kính BC
Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF
∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^
∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)
=> ME=AH:2= MH do đó ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^
Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)
Nên O E B ^ + M E H ^ = 90 0 Suy ra M E O ^ = 90 0
⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^ = DFC ^
Tứ giác AFDC có A F C ^ = A D C ^ = 90 0 nên tứ giác AFDC nội tiếp đường tròn => B D F ^ = B A C ^
∆ BDF và ∆ BAC có B D F ^ = B A C ^ (cmt); B ^ chung do đó ∆ BDF ~ ∆ BAC(g-g)
Chứng minh tương tự ta có ∆ DEC ~ ∆ ABC(g-g)
Do đó ∆ DBF ~ ∆ DEC ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)
Vì ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác ⇒ D I D F = D J D C (2)
Từ (1) và (2) suy ra ∆ DIJ ~ ∆ DFC (c-g-c) => DIJ ^ = DFC ^

\({}\)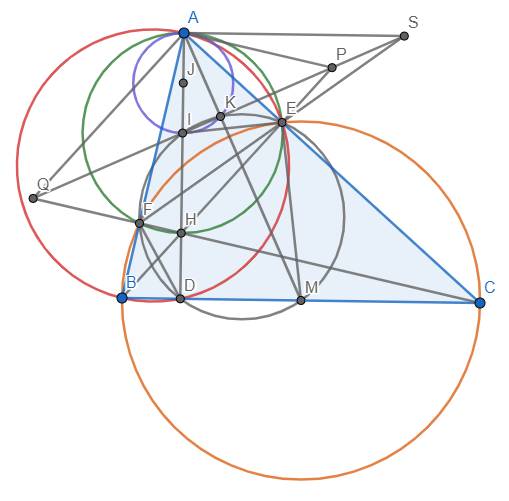
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)

Ta có: ΔEAH vuông tại E
mà EI là đường trung tuyến
nên IE=IH
=>ΔIEH cân tại I
=>\(\widehat{IHE}=\widehat{IEH}\)
mà \(\widehat{IHE}=\widehat{BHD}\)(hai góc đối đỉnh)
và \(\widehat{BHD}=\widehat{BCE}\left(=90^0-\widehat{EBC}\right)\)
nên \(\widehat{IEH}=\widehat{BCE}\)
Ta có: ΔEBC vuông tại E
mà EO là đường trung tuyến
nên OE=OB
=>ΔOEB cân tại O
=>\(\widehat{OEB}=\widehat{OBE}\)
Ta có: \(\widehat{IEO}=\widehat{IEH}+\widehat{OEH}\)
\(=\widehat{EBC}+\widehat{ECB}=90^0\)
=>ΔIEO vuông tại E
Ta có: ΔAFH vuông tại F
mà FI là đường trung tuyến
nên FI=IH
=>FI=IE
=>I nằm trên đường trung trực của FE(1)
Ta có: ΔBFC vuông tại F
mà FO là đường trung tuyến
nên \(FO=\dfrac{BC}{2}\)
mà EO=BC/2
nên FO=EO
=>O nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra IO là đường trung trực của EF
=>IO\(\perp\)EF tại K và K là trung điểm của FE
Xét ΔIEO vuông tại E có EK là đường cao
nên \(IK\cdot IO=IE^2\)
=>\(IK\cdot IO=\left(\dfrac{1}{2}AH\right)^2=\dfrac{1}{4}AH^2\)
=>\(AH^2=4\cdot IK\cdot IO\)
Bài giải:
Sao EF lại vuông với BC được lại còn suy ra EF vuông với BC