Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có hai đáp số tương ứng với hai vị trí của điểm D
*Trường hợp D nằm giữa C và B
VÌ C nằm chính giữa A và B nên :


Trường hợp 1: D nằm giữa A và C
=>\(\widehat{AOD}=90^0-60^0=30^0\)
=>\(\widehat{DOB}=150^0\)
Trường hợp 2: D nằm giữa B và C
ΔOCD cân tại O có CD=OC
nên ΔOCD đều
=>\(\widehat{COD}=60^0\)
hay \(\widehat{BOD}=30^0\)

Do \(OC=OD=CD=R\Rightarrow\Delta OCD\) là tam giác đều
\(\Rightarrow\widehat{COD}=60^0\)
Mà \(\widehat{CAD}=\dfrac{1}{2}\widehat{COD}\) (góc nt và góc ở tâm cùng chắn CD)
\(\Rightarrow\widehat{CAD}=30^0\)
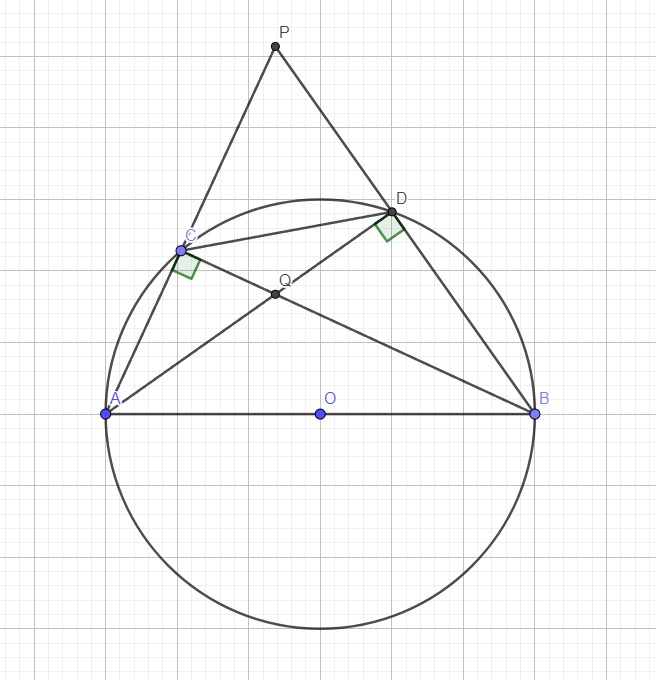
AB là đường kính nên \(\widehat{ADB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{ADP}=90^0\Rightarrow\widehat{APB}=180^0-\left(90^0+30^0\right)=60^0\)
Tương tự ta có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\Rightarrow\widehat{BCP}=90^0\)
\(\Rightarrow\widehat{CQD}=360^0-\left(\widehat{APB}+\widehat{ADP}+\widehat{ACB}\right)=360^0-\left(60^0+90^0+90^0\right)=120^0\)
\(\Rightarrow\widehat{AQB}=\widehat{CQD}=120^0\) (2 góc đối đỉnh)
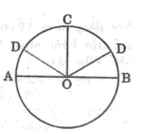
Xét tam giác COD có:
OC=OD=CD=R
=> tam giác COD là tam giác đều
=> góc COD=60 độ (t/c tam giác đều)
Mà cung CD= góc COD= 60 độ ( góc COD là góc ở tâm chắn cung CD)
=> sđ cung CD= 60 độ
* Xét trường hợp điểm D gần điểm B
=> D thuộc cung BC
=> sđ cung BC= sđ cung CD= sđ cung BD (1)
Ta lại có điểm C là điểm nằm chính giữa cung AB (gt)
=> sđ cung AC= sđ cung BC= sđ cung AB/2= 180 độ/2= 90 độ
Thay vào (1) ta có:
90 độ= 60 độ+ sđ cung BD
=> sđ cung BD= 90 độ - 60 độ= 30 độ
* Xét trường hợp điểm D nằm gần điểm A
=> C thuộc cung BD
=> sđ cung BD= sđ cung BC+ sđ cung CD
=> sđ cung BD= 90 độ + 60 độ= 150 độ