Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
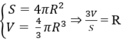

Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
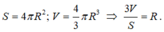

Câu 5:
Tương tự câu 4, ta thấy tâm $I$ của khối cầu ngoại tiếp $S.ABCD$ là trung điểm $SC$
Theo định lý Pitago:
$SA^2=SB^2-AB^2=(a\sqrt{3})^2-a^2=2a^2$
$AC^2=AB^2+BC^2=a^2+a^2=2a^2$
$SC=\sqrt{SA^2+AC^2}=\sqrt{2a^2+2a^2}=2a$
Do đó: $R=SI=IC=\frac{SC}{2}=a$
Thể tích khối cầu ngoại tiếp S.ABCD là:
$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi a^3$
Đáp án A
Câu 4:
$AC=\sqrt{AB^2+AD^2}=2a$
$(SC, (ABCD))=\widehat{SCA}=60^0$
$\Rightarrow \frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{3}.AC=2\sqrt{3}a$
$SC=\sqrt{SA^2+AC^2}=\sqrt{(2\sqrt{3}a)^2+(2a)^2}=4a$
Gọi $I$ tâm mặt cầu ngoại tiếp hình chóp. $IS=IA=IC$ nên $I$ là tâm ngoại tiếp tam giác $SAC$
$\Rightarrow I$ là trung điểm $SC$.
Bán kính $IS=IC=\frac{AC}{2}=\frac{4a}{2}=2a$
Đáp án A



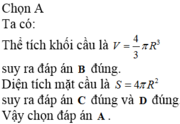
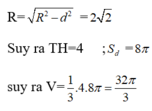


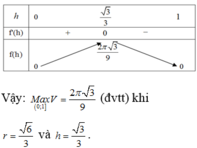
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là: