Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình hướng dẫn thế này để bạn tự tính nhé.
a. \(\omega\) thay đổi để UR max khi hiện tượng cộng hưởng xảy ra \(\Rightarrow\omega=\frac{1}{\sqrt{LC}}\)
b. \(\omega\) thay đổi để UL max khi \(\omega=\frac{1}{X.C}\), với \(X=\sqrt{\frac{L}{C}-\frac{R^2}{2}}\)
c. \(\omega\) thay đổi để Uc max khi \(\omega=\frac{X}{L}\) với X ở câu b.

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
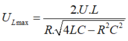
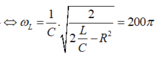
Và điện áp trên tụ cực đại là:
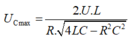
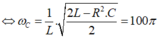
Dễ thấy:
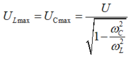
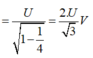

Khi L = L 1 điện áp hiệu dụng trên tụ cực đại → cộng hưởng, khi đó U = U R = 200 V .
Khi L = L 2 điện áp trên cuộn dây cực đại, ta có U R C = U L m a x 2 − U 2 = 189 V .
→ Điện áp hiệu dụng trên tụ U C = U R C 2 − U R 2 = 135 V .
Đáp án B

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có:
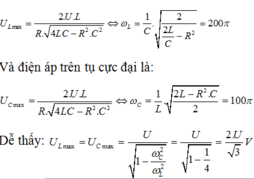

Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Khi điện áp hiệu dụng ở hai đầu cuộn dây cực đại thì u vuông pha với u R C → U R C = U L m a x 2 − U 2 = 3 U = 3 (chuẩn hóa U = 1).
Mặc khác U R U L m a x = U U R C ⇒ U R = U U R C U L m a x = 3 2
→ Hệ số công suất của mạch khi bỏ cuộn dây cos φ = U R U R C = 1 2
Đáp án A

Chọn D.
Khi cho f = f1 thì điện áp hiệu dụng giữa hai đầu tụ và hai điện trở bằng nhau.
Chọn Z C 1 = 1 ⇒ R = 1 , Z L 1 = x .
Khi cho d = 1,5f1 thì điện áp hiệu dụng giữa hai đầu cuộn cảm và hai đầu điện trở bằng nhau ⇒ Z L 2 = 1 , 5 x ⇒ Z L 2 = R ⇒ 1 , 5 x = 1 ⇔ x = 2 3 .
Thay đổi f = f3 = nf1 để giữa hai đầu cuộn cảm đạt cực đại ⇒ Z L 3 = 2 n 3 , Z C 3 = 1 n .
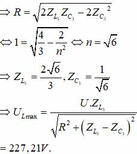
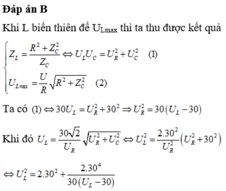
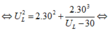
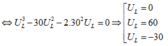
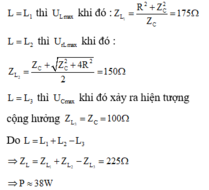
\(Z_C=\frac{1}{\omega C}=100\Omega\)
a. Để điện áp giữa hai đầu điện trở cùng pha với 2 đầu mạch thì u cùng pha với i --> \(Z_L=Z_C=100\Omega\)
\(\omega L=100\Rightarrow L=\frac{1}{\pi}\left(H\right)\)
b. L thay đổi để UL max khi:
\(Z_L=\frac{R^2+Z_C^2}{Z_C}=\frac{100^2+100^2}{100}=200\Omega\)
\(U_{Lmax}=U\frac{\sqrt{R^2+Z_C^2}}{R}=220V\)
Sao ra UL max bằng 220 thế Trần Hoàng Sơn