Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 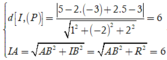
![]()
hay A là hình chiếu vuông góc của I trên mặt phẳng (P)
Do đó ta dễ dàng tìm được ![]()
Chọn B.

Đáp án B
Phương pháp:
Tính bán kính hai khối cầu dựa vào các mối quan hệ đường tròn nội tiếp tam giác.
Tính thể tích hai khối cầu đã cho theo công thức V = 4 3 π . R 3 và suy ra kết luận.
Cách giải: Cắt món đồ chơi đó bằng mặt phẳng đứng đi qua trục hình nón.
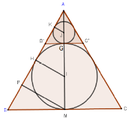
Gọi P, H, K lần lượt là hình chiếu vuông góc của M, I, J trên AB.
Vì B A C = 2 β = 60 ° , A M = 9 c m .
⇒ B M = M C = 3 3 A B = A C = 6 3 = B C ⇒ Δ A B C đều.
Vì IM là bán kính mặt cầu nội tiếp tam giác đều ABC nên I H = I M = A M 3 = 3
Gọi là tiếp tuyến chung của hai đường tròn. Vì Δ A B C đều nên dẫn đến Δ A B ' C ' đều.
Suy ra bán kính đường tròn nội tiếp:
J K = J G = A G 3 = A M 9 = 1
Vậy tổng thể tích là:
V 1 + V 2 = 4 3 π . I H 3 + 4 3 π . J K 3 = 112 π 3
Chú ý khi giải:
Cần chú ý vận dụng các mối quan hệ đường tròn nội, ngoại tiếp tam giác đều trong việc tính bán kính các khối cầu.



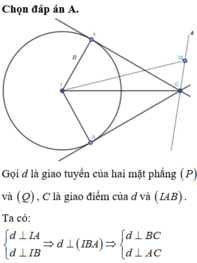



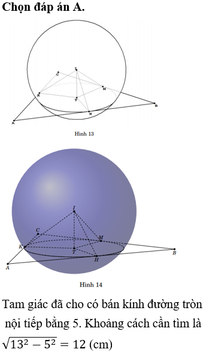


Đáp án A
Ta có