Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

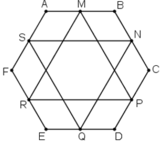
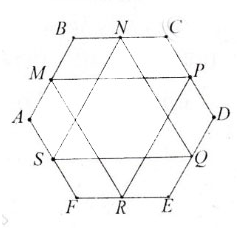
Gọi G là trọng tâm tam giác MPR 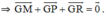
Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh 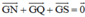
Thật vậy ta có:
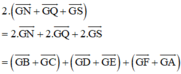
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
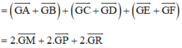
(Vì M, P, R là trung điểm AB, CD, EF)
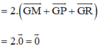
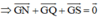 hay G cũng là trọng tâm của ΔNQS.
hay G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.

Giải:
Gọi \(G\) là trọng tâm của \(\Delta MPR\) và \(K\) là trọng tâm của của \(\Delta NQS\)
\(\Rightarrow\) Ta cần chứng minh: \(K\) và \(G\) trùng nhau
Vì \(G\) là trọng tâm của \(\Delta MPR\) nên ta có:
\(3\overrightarrow{KG}=\overrightarrow{KM}+\overrightarrow{KP}+\overrightarrow{KR}\)
\(=\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}+\overrightarrow{KD}+\overrightarrow{KE}+\overrightarrow{KF}\right)\) (t/c trung điểm)
\(=\dfrac{1}{2}\left(\overrightarrow{KB}+\overrightarrow{KC}\right)+\dfrac{1}{2}\left(\overrightarrow{KD}+\overrightarrow{KE}\right)+\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KF}\right)\)
\(=\overrightarrow{KN}+\overrightarrow{KQ}+\overrightarrow{KS}=\overrightarrow{0}\) (Vì \(K\) là trọng tâm của của \(\Delta NQS\))
\(\Rightarrow\) Đpcm

A B C D M N P Q
Gọi G lần lượt là trọng tâm tam giác ANP. Ta sẽ chứng minh G cũng là trọng tâm tam giác MQC.
Ta có: \(\overrightarrow{GA}+\overrightarrow{GN}+\overrightarrow{GB}=\overrightarrow{0}\).
Ta cần chứng minh: \(\overrightarrow{GC}+\overrightarrow{GM}+\overrightarrow{GQ}=\overrightarrow{0}\).
Thật vậy: \(\overrightarrow{GC}+\overrightarrow{GM}+\overrightarrow{GQ}=\overrightarrow{GA}+\overrightarrow{AC}+\overrightarrow{GN}+\overrightarrow{NM}+\overrightarrow{GP}+\overrightarrow{PQ}\)
\(=\left(\overrightarrow{GA}+\overrightarrow{GN}+\overrightarrow{GP}\right)+\left(\overrightarrow{AC}+\overrightarrow{NM}+\overrightarrow{PQ}\right)\)
\(=\overrightarrow{0}+\overrightarrow{AC}+\overrightarrow{NM}+\overrightarrow{PQ}\).
Do các điểm M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên PQ và NM lần lượt là các đường trung bình của tam giác DAC và BAC.
Vì vậy: \(\overrightarrow{NM}=\dfrac{1}{2}\overrightarrow{CA};\overrightarrow{PQ}=\dfrac{1}{2}\overrightarrow{CA}\).
Ta có: \(\overrightarrow{AC}+\overrightarrow{NM}+\overrightarrow{PQ}=\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CA}=\overrightarrow{0}\).
Ta chứng minh được: \(\overrightarrow{GC}+\overrightarrow{GM}+\overrightarrow{GQ}=\overrightarrow{0}\) nên G là trọng tâm tam giác CMQ.
Vậy hai tam giác ANP và CMQ có cùng trọng tâm.

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm

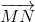 =
= 
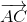
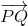 =
=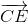
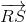 =
= 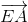
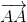 =
= 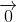
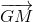 +
+ 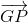 +
+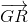 =
= 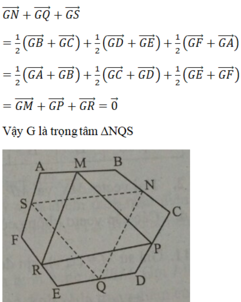
 hinh hơi rối bạn thông cảm nhé.
hinh hơi rối bạn thông cảm nhé.
Ta có :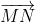 =
= 
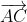
=>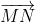 +
+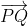 +
+ =
=  (
(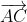 +
+ +
+ ) =
) = 
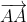 =
= 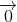
=>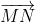 +
+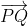 +
+ =
=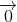 (1)
(1)
Gọi G là trong tâm của tam giác MPR, ta có:
Mặt khác :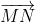 =
= 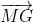 +
+