Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|\overrightarrow{a}+\overrightarrow{b}\right|^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)
\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}.\overrightarrow{b}\)
\(=5^2+12^2+2.5.12.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\)
\(=169+120cos\left(\overrightarrow{a},\overrightarrow{b}\right)=13^2\)
Suy ra: \(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=0\).
\(\overrightarrow{a}\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left(\overrightarrow{a}\right)^2+\overrightarrow{a}.\overrightarrow{b}=5^2+5.12.0=25\).
Mặt khác \(\overrightarrow{a}\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|.\left|\overrightarrow{a}+\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\)
\(=5.13.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\).
Vì vậy \(25=5.13.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\).
\(cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)=\dfrac{5}{13}\).
Vậy góc giữa hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{a}+\overrightarrow{b}\) là \(\alpha\) sao cho \(cos\alpha=\dfrac{5}{13}\).

a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).

a) \(\overrightarrow{a}+\overrightarrow{b}=\left(2;-2\right)+\left(1;4\right)=\left(3;2\right)\).
\(\overrightarrow{a}-\overrightarrow{b}=\left(2;-2\right)-\left(1;4\right)=\left(1;-6\right)\).
\(2\overrightarrow{a}+3\overrightarrow{b}=2\left(2;-2\right)+3\left(1;4\right)=\left(4;-4\right)+\left(3;12\right)\)\(=\left(7;8\right)\).
c) Gọi x và y là hai số thực để:
\(\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x\left(2;-2\right)+y\left(1;4\right)=\left(2x+y;-2x+4y\right)\)
Từ đó suy ra: \(\left\{{}\begin{matrix}2x+y=5\\-2x+4y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\).
Vậy \(\overrightarrow{c}=2\overrightarrow{a}+1\overrightarrow{b}\).

a) Đúng
b) Sai vì: \(\overrightarrow{a}+\overrightarrow{b}=\left(0;2\right)\ne\overrightarrow{0}\).
c) Sai vì \(\overrightarrow{a}+\overrightarrow{b}=\left(7;7\right)\ne\overrightarrow{0}\)

a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy câu a) đúng.
b) Câu này cũng đúng.

a) Theo giả thiết \(\overrightarrow{a}=\overrightarrow{b}\ne\overrightarrow{0}\) nên giả sử \(\overrightarrow{a}=m\overrightarrow{b}\) suy ra:
\(\overrightarrow{a}=m\overrightarrow{a}\Leftrightarrow\left(1-m\right)\overrightarrow{a}=\overrightarrow{0}\).
\(\Leftrightarrow1-m=0\) (vì \(\overrightarrow{a}\ne\overrightarrow{0}\) ).
\(\Leftrightarrow m=1\).
b) Nếu \(\overrightarrow{a}=-\overrightarrow{b};\overrightarrow{a}\ne\overrightarrow{0}\).
Giả sử \(\overrightarrow{a}=m\overrightarrow{b}\Leftrightarrow\overrightarrow{a}=-m\overrightarrow{a}\)\(\Leftrightarrow\overrightarrow{a}\left(1+m\right)=\overrightarrow{0}\)
\(\Leftrightarrow1+m=0\)\(\Leftrightarrow m=-1\).
c) Do \(\overrightarrow{a}\) , \(\overrightarrow{b}\) cùng hướng nên: \(m>0\).
Mặt khác: \(\overrightarrow{a}=m\overrightarrow{b}\Leftrightarrow\left|\overrightarrow{a}\right|=\left|m\right|.\left|\overrightarrow{b}\right|\)
\(\Leftrightarrow20=5.\left|m\right|\)\(\Leftrightarrow\left|m\right|=4\)
\(\Leftrightarrow m=\pm4\).
Do m > 0 nên m = 4.
d) Do \(\overrightarrow{a},\overrightarrow{b}\) ngược hướng nên m < 0.
\(\left|\overrightarrow{a}\right|=\left|m\right|.\left|\overrightarrow{b}\right|\)\(\Leftrightarrow15=\left|m\right|.3\)\(\Leftrightarrow\left|m\right|=5\)\(\Leftrightarrow m=\pm5\).
Do m < 0 nên m = -5.
e) \(\overrightarrow{a}=\overrightarrow{0};\overrightarrow{b}\ne\overrightarrow{0}\) nên\(\overrightarrow{0}=m.\overrightarrow{b}\). Suy ra m = 0.
g) \(\overrightarrow{a}\ne\overrightarrow{0};\overrightarrow{b}=\overrightarrow{0}\) nên \(\overrightarrow{a}=m.\overrightarrow{0}=\overrightarrow{0}\). Suy ra không tồn tại giá trị m thỏa mãn.
h) \(\overrightarrow{a}=\overrightarrow{0};\overrightarrow{b}=\overrightarrow{0}\) nên \(\overrightarrow{0}=m.\overrightarrow{0}\). Suy ra mọi \(m\in R\) đều thỏa mãn.

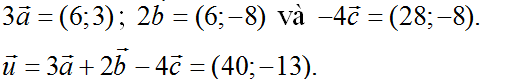
Từ = 0, ta có
= 0, ta có 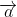 +
+ 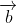 = 0 =>
= 0 => 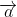 = -
= -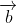
Điều này chứng tỏ hai vectơ có cùng độ dài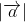 =
=  , cùng phương và ngược hướng
, cùng phương và ngược hướng
toán cx copy mạng hả pn