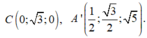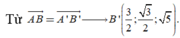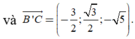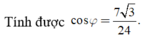Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

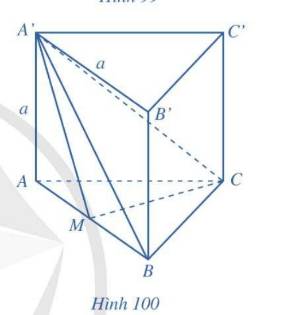
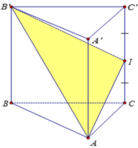
a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)

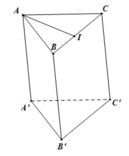
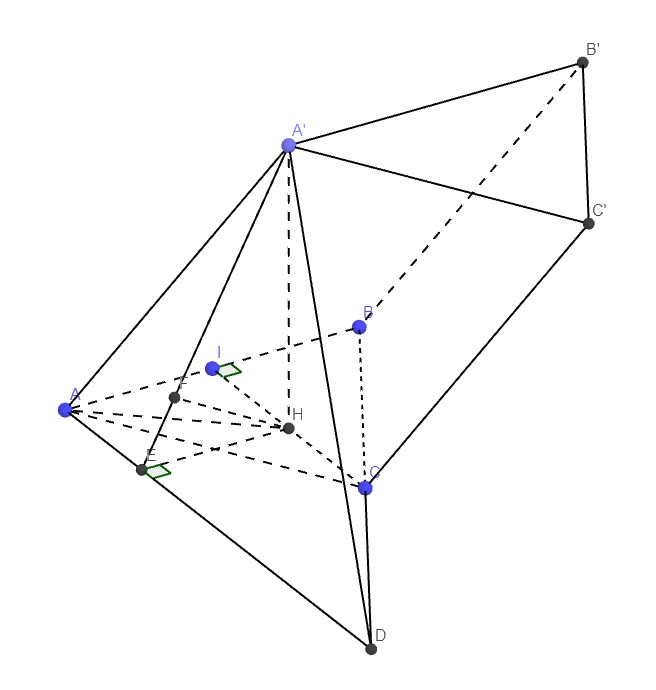
Qua A kẻ đường thẳng song song CI cắt BC kéo dài tại D
\(\Rightarrow CI||\left(A'AD\right)\Rightarrow d\left(A'A;CI\right)=d\left(CI;\left(A'AD\right)\right)=d\left(H;\left(A'AD\right)\right)\)
Từ H kẻ \(HE\perp AD\), từ H kẻ \(HF\perp A'E\)
\(\Rightarrow HF\perp\left(A'AD\right)\Rightarrow HF=d\left(H;\left(A'AD\right)\right)\)
Tứ giác AIHE là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AI=\dfrac{a}{2}\)
\(A'H\perp\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(A'A\) là (ABC)
\(\Rightarrow\widehat{A'AH}=45^0\)
\(CI=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow IH=\dfrac{1}{2}CI=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow AH=\sqrt{AI^2+IH^2}=\dfrac{a\sqrt{7}}{4}\)
\(\Rightarrow A'H=AH.tan45^0=\dfrac{a\sqrt{7}}{4}\)
Hệ thức lượng:
\(HF=\dfrac{HE.A'H}{\sqrt{HE^2+A'H^2}}=\dfrac{a\sqrt{77}}{22}\)

Đáp án A.
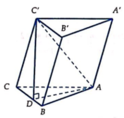
Theo giả thiết ta có CD' ⊥ (ABC). Áp dụng định lý Cô-sin cho ∆ ABD ta được:
AD = ![]()
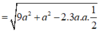
![]()
Hình chiếu vuông góc của AC’ trên mặt phẳng (ABC) là AD, vì vậy ta có góc giữa AC' và mặt phẳng (ABC) là góc C ' A D ^ = 45 0 => ∆ C'AD vuông cân tại D
![]()
Diện tích
∆
ABC là 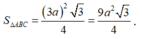
Do đó 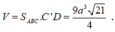

Đáp án A
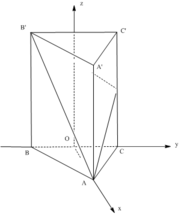
Gắn hệ trục tọa độ Oxyz như hình vẽ
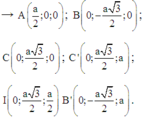
Vecto pháp tuyến của mặt phẳng
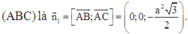
Vecto pháp tuyến của mặt phẳng (AB’I) là
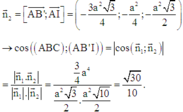

Chọn D

Gọi N, K là trung điểm của BB', A'B'
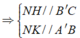
![]()
Ta tính được
![]()
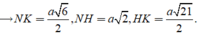
Áp dụng định lí hàm cosin ta suy ra

Cách 2. Chọn hệ trục tọa độ Oxyz với
![]()