Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

làm đc chưa bạn...
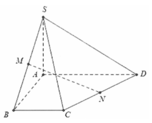
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

Đáp án C
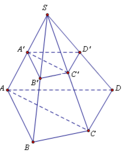
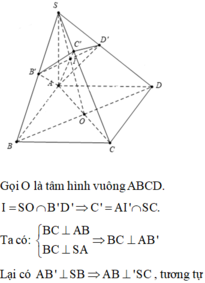
Ta có: V S . A ' B ' C ' V S . A B C = S A ' S A . S B ' S B . S C ' S C = 1 2 . 1 2 . 1 2 = 1 8
⇒ V S . A ' B ' C ' = 1 8 V S . A B C 1
V S . A ' D ' C ' V S . A D C = S A ' S A . S D ' S D . S C ' S C = 1 2 . 1 2 . 1 2 = 1 8
⇒ V S . A ' D ' C ' = 1 8 V S . A D C 2
Từ (1) và (2) ⇒ V S . A ' B ' C ' D ' = V S . A ' B ' C ' + V S . A ' D ' C ' = 1 8 V S . A B C + V S . A D C
= 1 8 V S . A B C D ⇒ V S . A ' B ' C ' D ' V S . A B C D = 1 8

Đáp án C
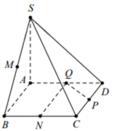
Ta có
S Q P C N = S A B C D − S A B N Q − S Δ P Q D = S A B C D − 1 2 S A B C D − 1 8 S A B C D = 3 8 S A B C D .
Khi đó
V M . Q P C N = 1 3 . d M ; A B C D . S Q P C N = 1 3 . 1 2 . d S ; A B C D . 3 8 . S A B C D = 3 16 . 1 3 . d S ; A B C D . S A B C D = 3 16 . V 0 .
Vậy V = 3 16 V 0 .

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)
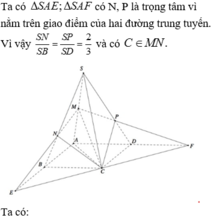
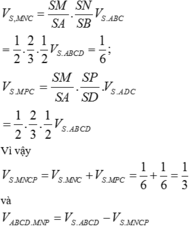



Đáp án A