Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


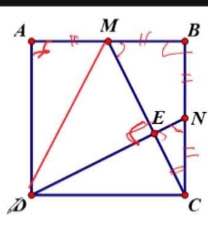
a, Chứng minh ∆CMB = ∆DNC => N C E ^ = C D N ^
Từ đó chứng minh được C E N ^ = 90 0
b, Ta có A,D,E,M cùng thuộc được tròn đường kính DM
c, Gọi I là trung điểm của CD, chứng minh AI song song với MC
=> ∆ADE cân tại A
=> B,E,D cùng thuộc (A;AB)

a: ta có: \(MA=MB=\frac{AB}{2}\)
\(BN=NC=\frac{BC}{2}\)
mà BA=BC
nên MA=MB=BN=NC
Xét ΔNCD vuông tại C và ΔMBC vuông tại B có
NC=MB
CD=BC
Do đó: ΔNCD=ΔMBC
=>\(\hat{CND}=\hat{BMC}\)
mà \(\hat{BMC}+\hat{BCM}=90^0\) (ΔBCM vuông tại B)
nên \(\hat{CND}+\hat{BCM}=90^0\)
=>CM⊥DN tại E
=>\(\hat{CEN}=90^0\)
b: ta có: \(\hat{MAD}=90^0\)
=>A nằm trên đường tròn đường kính MD(1)
Ta có: \(\hat{MED}=90^0\)
=>E nằm trên đường tròn đường kính MD(2)
Từ (1),(2) suy ra A,E,M,D cùng thuộc một đường tròn

a: ta có: \(MA=MB=\frac{AB}{2}\)
\(BN=NC=\frac{BC}{2}\)
mà BA=BC
nên MA=MB=BN=NC
Xét ΔNCD vuông tại C và ΔMBC vuông tại B có
NC=MB
CD=BC
Do đó: ΔNCD=ΔMBC
=>\(\hat{CND}=\hat{BMC}\)
mà \(\hat{BMC}+\hat{BCM}=90^0\) (ΔBCM vuông tại B)
nên \(\hat{CND}+\hat{BCM}=90^0\)
=>CM⊥DN tại E
=>\(\hat{CEN}=90^0\)
b: ta có: \(\hat{MAD}=90^0\)
=>A nằm trên đường tròn đường kính MD(1)
Ta có: \(\hat{MED}=90^0\)
=>E nằm trên đường tròn đường kính MD(2)
Từ (1),(2) suy ra A,E,M,D cùng thuộc một đường tròn