Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N P 1 2 K H 2 H 1
a) Ta có DM song song và bằng BN nên BMDN là hình bình hành (vì có 2 cạnh đối song song và bằng nhau)
b) Tam giác CDN bằng tam giác DAP (cạnh - góc - cạnh)
=> Góc D1 = góc A1
Ta lại có Góc D2 + Góc D1 = Góc D = 90 độ
=> Góc D2 + Góc A1 = 90 đo
Trong tam giác KAD có tổng 2 góc A và D bằng 90 độ nên góc K bằng 90 độ
=> AP vuông góc với DN
c) Tương tự câu b ta có BM vuông góc với AP
=> BM // DN (vì cùng vuông góc vời AP)
=> BMKN là hình thang.
Theo câu b tam giác KAD vuông tại K có KM là trung tuyến ứng với cạnh huyền => KM = 1/2 AD
=> KM = BN
=> BMKN là hình thang cân
d) \(DP=\frac{1}{2}\sqrt{5},AP=\sqrt{5-\frac{1}{4}5}=\frac{\sqrt{15}}{2}\)
\(DP^2=PK.PA\)
=> \(PK=\frac{DP^2}{PA}=\frac{\frac{5}{4}}{\frac{\sqrt{15}}{2}}=\frac{\sqrt{15}}{6}\)
=> \(\frac{PK}{PA}=\frac{\frac{\sqrt{15}}{6}}{\frac{\sqrt{15}}{2}}=\frac{1}{3}\)
=> Đường cao hạ từ K xuống DC bằng 1/3 đường cao hạ từ A xuống DC
=> Đường cao hạ từ K xuống DC = \(\frac{1}{3}\sqrt{5}\)
=> Đường cao hạ từ K xuống MN bằng \(\frac{1}{2}\sqrt{5}-\frac{1}{3}\sqrt{5}=\frac{\sqrt{5}}{6}\)
=> Diện tích KMN bằng \(\frac{1}{2}.MN.KH_2=\frac{1}{2}\sqrt{5}\frac{\sqrt{5}}{6}=\frac{5}{12}\)

https://olm.vn/hoi-dap/detail/96788252350.html
Tham khảo ở link này (mình gửi cho)
Hoc tốt!!!!!!!!!!!!

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

GIÚP MÌNH ĐI! GẤP LĂM! SÁNG 9/12/2018 LÀ MÌNH PHẢI NỘP RỒI.
A B C D M N I K E N P a) MN là dường trung bình tam giác ABD,PE là đường trung bình tam giác ACD=>MN//AD,PQ//AD=>PE//MN.
tương tự, ta có: NQ//MP. ==>MNQP laf hbh.
b) IP là đường trung bình tam giác ADC=>IP //CD, KN là đường trung bình tam giác BDC=>KN //CD, IK là đường trung bình hình thang ABCD=>IK //CD .==>NP // CD(theo tiên đề ơ-clit).
còn câu c bạn cố gắng nha, khuya quá mẹ mk bắt ngủ nên ko ghi rõ ra, phần đường trung bình là do có các trung điểm đã cho. thông cảm nha

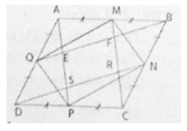
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2

a,Hình bình hành ABCD có AB=CD
⇒12AB=AM=12CD=CN⇒12AB=AM=12CD=CN
Mặt khác, M,N lần lượt là trung điểm của AB và CD
Do đó, AM//CN
Tứ giác AMCN có cặp cạnh đối vừa song song vừa bằng nhau nên là hình bình hành (đpcm)
b, Tứ giác AMCN là hình bình hành
⇒⇒M1ˆ=N1ˆM1^=N1^ (Hai góc đối của hình bình hành AMCN)
⇒⇒M2ˆ=N2ˆM2^=N2^ (Do M1ˆM1^ và M2ˆM2^ là hai góc kề bù; N1ˆN1^ và N2ˆN2^ là hai góc kề bù)
Mặt khác, ABCD là hình bình hành nên AB//CD ⇒⇒B1ˆ=D1ˆB1^=D1^
ΔEDNΔEDN và ΔKBMΔKBM có:
M2ˆ=N2ˆM2^=N2^
DN=BMDN=BM
B1ˆ=D1ˆB1^=D1^
⇒ΔEDN=ΔKBM(g.c.g)⇒ΔEDN=ΔKBM(g.c.g)
⇒ED=KB⇒ED=KB (đpcm)
c, Gọi O là giao điểm của AC và BD.
ABCD là hình bình hành
⇒OA=OC⇒OA=OC
ΔCABΔCAB có:
MA=MBMA=MB
OA=OCOA=OC
MC cắt OB tại K
⇒⇒ K là trọng tâm của ΔCABΔCAB
Mặt khác, I là trung điểm của BC
⇒⇒ IA,OB,MC đồng quy tại K
Hay AK đi qua trung điểm I của BC (đpcm)

a) Xét tam giác ACD có: AF=FC (gt) ; DK=KC (gt)
=> FK là đường trung bình của tam giác ACD
=> FK//AD
=> ADKF là hình thang
Chứng minh tương tự t cũng có: ME là đường trung bình của tam giác ABD
=> ME // AD mà FK//AD (cmt)
=> ME//FK (1)
Chứng minh tương tự ta cũng có:
MF là đường trung bình tam giác ABC , EK là đường trung bình tam giác DBC
=> MF//BC ; EK // BC
=> MF//EK (2)
Từ (1) và (2) ta có: EMFK là hình bình hành