Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài ta có :AM = 1/2 AD nên AM bằng 1/2 BC , Ta có :
sAMB = 1/2 sBMC hay sBMC = 2 nhân sAMB
b] sBMC =2nhân sAMB , mà hai tam giác chung đáy MB nên chiều cao CI gấp đôi chièu cao AH
Tam giác BNC và ANC có chung đáy NB , chiều cao CI = 2 nhân AH
Suy sBNC = 2 nhân sANB
sABC = 1/2 sABCD
sABC = 1,5 * ( 1 + 2) = 4,5 dm 2
sABCD =4,5 * 2= 9 dm2
sABCD = 4,5 * 2 = 9

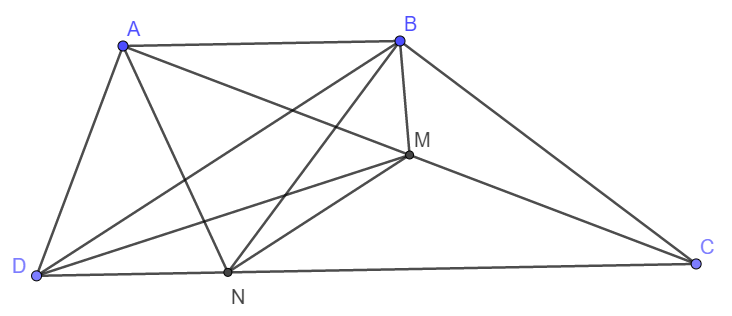
a) Ta thấy hai tam giác MN và DMN có chung cạnh MN.
Lại có do DB // MN nên chiều cao hà từ B và D xuống MN là bằng nhau.
Vậy diện tích tam giác BNM bằng diện tích tam giác DMN.
b) Ta thấy \(AM=MC\Rightarrow\frac{S_{ABM}}{S_{BAC}}=\frac{1}{2};\frac{S_{ADM}}{S_{DAC}}=\frac{1}{2}\)
Vậy nên \(\frac{S_{ABM}+S_{ADM}}{S_{BAC}+S_{DAC}}=\frac{1}{2}\Rightarrow\frac{S_{ABMD}}{S_{ABCD}}=\frac{1}{2}\)
\(\Rightarrow S_{ABMD}=16:2=8\left(cm^2\right)\)
Lại có \(S_{ABMD}=S_{ABMND}-S_{DMN}=S_{ABND}+S_{BMN}-S_{DMN}\)
\(=S_{ABND}\) hay \(S_{ABND}=8cm^2\)


a) Ta thấy tam giác BMC có đáy BC và chiều cao bằng AB
Tam giác AMB có đáy AM và chiều cao AB
Lại có BC = AD = 2AM nên diện tích tam giác BMC gấp 2 lần diện tích tam giác AMB.
b) Ta thấy tam giác BNC và tam giác BNA chung chiều cao nên \(\frac{S_{BNC}}{S_{BNA}}=\frac{NC}{AN}\)
Tam giác MCN và tam giác MAN chung chiều cao nên \(\frac{S_{MCN}}{S_{MAN}}=\frac{NC}{AN}\)
Vậy nên \(\frac{S_{ABC}}{S_{AMC}}=\frac{NC}{AN}\)
Mà ta thấy tam giác ABC và tam giác AMC có chiều cao bằng nhau, BC = 2AM nên \(\frac{S_{ABC}}{S_{AMC}}=2\Rightarrow\frac{NC}{AN}=2\)
Tam giác BNC và tam giác ANB có chung chiều cao nên \(\frac{S_{BNC}}{S_{ANB}}=\frac{NC}{AN}=2\)
Ta có \(\frac{S_{BNC}}{S_{ANB}}=2\Rightarrow\frac{S_{ABC}}{S_{ANB}}=3\Rightarrow\frac{S_{ABCD}}{S_{ANB}}=6\)
Vậy diện tích ABCD bằng: 1,5 x 6 = 9 (dm2)

a ) Chu vi hình vuông ABCD là :
12 x 4 = 48 ( cm )
Diện tích hình vuông ABCD là :
12 x 12 = 144 ( cm2 )
b ) Diện tích tam giác ABN bằng 1/2 diện tích hình vuông , vậy diện tích tam giác ABN là :
144 : 2 = 72 ( cm2 )
Tam giác BMN có đáy BM = 1/2 BC = 12 : 2 = 6 ( cm )
Và đường cao tương ứng là đoạn NC = 1/2 CD = 12 : 2 = 6 ( cm )
Diện tích tam giác BMN bằng :
6 x 6 : 2 = 18 ( cm2 )
Vì 72/18 = 4 nên diện tích tam giác ABN gấp 4 lần diện tích tam giác BMN .
c) dt AMN = dt ABCD - ( dt ABM + dt MCN + dt ADN )
= 144 - ( 36 + 18 + 36 )
= 54 cm2 .
Hai tam giác ABN và BMN có cùng đáy NB mà dt ABN gấp 4 lần dt BMN nên đường cao hạ từ đỉnh A gấp 4 lần đường cao hạ từ đỉnh M .
Xét hai tam giác AON và MON có cùng đáy NO và đường cao hạ từ đỉnh A gấp 4 lần đường cao hạ từ đỉnh M nên dt tam giác AON gấp 4 lần dt tam giác MON .
Vậy dt tam giác AON là :
54 : ( 4 + 1 ) x 4 = 43,2 ( cm2 )
dt tứ giác AOND = dt tam giác AON + dt tam giác AND .
= 43 ,2 + 36
dt tứ giác AOND = 79,2 ( cm2 )
a: DM=AB/2=12cm
S ABMD=1/2(24+12)*24=12*36=432cm2
b: Xét ΔKMC và ΔKBA có
góc KMC=góc KBA
góc MKC=góc BKA
=>ΔKMC đồng dạng với ΔKBA
=>KM/KB=KC/KA=MC/AB=1/2
=>KC/KA=1/2
=>S ABK=2*S CBK
=>S ABK=192cm2
=>S ADMK=432-192=240cm2