Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay K(0) = 4 vào đa thức K(x) ta có : a.0^2 + b.0 + c => c = 4 (1)
Thay K(1) = 3 và (1) vào đa thức K(x) ta có : a.1^2 + b.1 + 4 = a + b + 4 = 3 => a+b=-1 => a= -1 - b (2)
Thay K(-1) = 7 , (1) vào đa thức K(x) ta có : a.(-1)^2 + b.(-1) + 4 = a-b+4=7 => a-b=3 (3)
Thay (2) vào (3) ta có : -1 - b - b = -1 - 2b = 3 => 2b= -4 => b = -2
Thay b = -2 vào (3) ta có : a - (-2) = 3 => a = 1.
Vậy a + b + c = 1 + (-2) + 4 = 3

Lời giải:
Ta có các điều sau:
\(\left\{\begin{matrix} a+b\equiv 0\pmod k\\ c+d\equiv 0\pmod k\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a\equiv -b\pmod k\\ d\equiv-c\pmod k\end{matrix}\right.\)
Áp dụng tính chất nhân của mo- đun:
\(\Rightarrow ad\equiv (-b)(-d)=bd\pmod k\) . Suy ra $ad-bc$ chia hết cho $k$
Do đó ta có đpcm

Chọn đáp án D
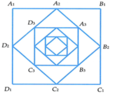
Cạnh của hình vuông A2B2C2D2 là A 2 B 2 = A 1 B 1 . 2 2
Cạnh của hình vuông A3B3C3D3 là
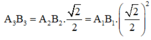
Cạnh của hình vuông A4B4C4D4 là

Tương tự, ta tính được cạnh của hình vuông A2018B2018C2018D2018 là
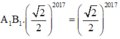
Chu vi của hình vuông
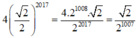

Đáp án A.
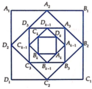
Từ giả thiết, ta có: A 2 B 2 = A 1 B 1 . 2 2 ; A 3 B 3 = A 2 B 2 . 2 = A 1 B 1 . 2 2 2 ;
A 4 B 4 = A 3 B 3 . 2 2 = A 1 B 1 . 2 2 3
Suy ra A k B k = A 1 B 1 . 2 2 k - 1 . Khi đó chu vi hình vuông A k B k C k D k được tính theo công thức P k = 4 A k B k = 4 A 1 B 1 . 2 2 k - 1 .
Vậy chu vi hình vuông A 2018 B 2018 C 2018 D 2018 là:
P 2018 = 4 A 1 B 1 . 2 2 2017 = 2 2 . 2 . 2 2018 2 2017 = 2 2 2017

\(\dfrac{1}{k^2}<\dfrac{1}{k(k-1)}=\dfrac{1}{k-1}-\dfrac{1}{k}\)
Ap dung:
\(\dfrac{1}{1^2}+\dfrac{1}{2^2}+\ldots+\dfrac{1}{n^2}<1+\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\ldots+\left(\dfrac{1}{n-1}-\dfrac{1}{n}\right)=2-\dfrac{1}{n}<2\)


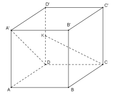
Đáp án A