Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình học kém lắm có biết gì đâu
Về cái này thì ko thể tiết lộ được

Bài 1: Gọi phân số đó là \(\dfrac{a}{b}\)
Ta có: \(\dfrac{200}{520}=\dfrac{5}{13}\)\(=>\dfrac{a}{b}=\dfrac{5k}{13k}\)
a) => a - b = 5k - 13k = 184
=> k.( 5 - 13 ) = 184
=> k.(-8) = 184 => k = -23
=> \(\dfrac{a}{b}=\dfrac{5.\left(-23\right)}{13.\left(-23\right)}=\dfrac{-115}{-229}\)
b) => a.b = 5k.13k = 9360
=> k^2.65 = 9360
=> k^2=144
=> \(\left[{}\begin{matrix}k^2=12^2\\k^2=-12^2\end{matrix}\right.=>\left[{}\begin{matrix}k=12\\k=-12\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}\dfrac{a}{b}=\dfrac{60}{156}\\\dfrac{a}{b}=\dfrac{-60}{-156}\end{matrix}\right.\)
Bài 2: a) đê A \(\in Z\) <=> n+1 \(⋮\) n-3
<=> n-3+4 \(⋮\) n-3 <=> 4 \(⋮\) n-3
<=> n-3 \(\in\) Ư(4)
<=> n-3 \(\in\) \(\left\{-1,1,-2,2,4,-4\right\}\)
<=> n \(\in\left\{2,4,1,5,7,-1\right\}\)
b) Gọi d là UCLN(n-1,n+3)
=> \(\left\{{}\begin{matrix}n-1⋮d\\n+3⋮d\end{matrix}\right.\)
=> \(n-1-\left(n+3\right)⋮d\)
=> \(n-1-n-3⋮d=>-4⋮d\)
=> d = 4
=> \(\left\{{}\begin{matrix}n-1\ne4k\\n+3\ne4k\end{matrix}\right.=>\left\{{}\begin{matrix}n\ne4k+1\\n\ne4k-3\end{matrix}\right.\) (để A tối giản)
Bài 3: Gọi a là tử của phân số cần tìm
Theo bài ra ta có : \(\dfrac{a}{15}=\dfrac{a-2}{15.2}=>\dfrac{a}{15}=\dfrac{a-2}{30}\)
=> 30a = 15.(a-2)
=> 30a = 15a - 30
=> 15a - 30a = 30
=> -15a = 30 => a = -2
=> Phân số cần tìm là: \(-\dfrac{2}{15}\)
Bài 4: do 10^11-1 < 10^12-1 => \(\dfrac{10^{11}-1}{10^{12}-1}< 1\)
Ta có:
\(\dfrac{10^{11}-1}{10^{12}-1}< \dfrac{10^{11}-1+11}{10^{12}-1+11}=\dfrac{10^{11}+10}{10^{12}+10}=\dfrac{10.\left(10^{10}+1\right)}{10.\left(10^{11}+1\right)}=\dfrac{10^{10}+1}{10^{11}+1}\)
=> \(\dfrac{10^{11}-1}{10^{12}-1}< \dfrac{10^{10}+1}{10^{11}+1}\)
Bài 5: \(\dfrac{1}{m}+\dfrac{n}{6}=\dfrac{1}{2}=>\dfrac{1}{m}=\dfrac{1}{2}-\dfrac{n}{6}=>\dfrac{1}{m}=\dfrac{3}{6}-\dfrac{n}{6}=>\dfrac{1}{m}=\dfrac{3-n}{6}\)
=> (3-n).m = 6
=> 3-n, m \(\inƯ\left(6\right)\)
Đến đây bn tự lập bảng giá trị nhé, mình hơi nhác![]()
Chúc bn học tốt

a) Nếu:
\(\dfrac{a}{b}< 1\Rightarrow\dfrac{a+m}{b+m}< 1\left(m\in Z\right)\)
\(\Rightarrow B=\dfrac{5^{12}+2}{5^{13}+2}< 1\)
\(B< \dfrac{5^{12}+2+48}{5^{13}+2+48}\Rightarrow B< \dfrac{5^{12}+50}{5^{13}+50}\Rightarrow B< \dfrac{5^2\left(5^{10}+2\right)}{5^2\left(5^{11}+2\right)}\Rightarrow B< \dfrac{5^{10}+2}{5^{11}+2}=A\)\(B< A\)
bạn ơi thế còn phần b thì sao? Mong bạn có câu trả lời sớm tớ cảm ơn bạn nhiều lắm

Ta xét từng trường hợp
+) Với a=1 ; \(n\in N\) => Có \(1^n\) với mọi n thuộc N thì đều bằng 1 ( thỏa mãn )
+) Với a=2 ; \(n\in N\) => Có \(2^n\) với mọi n tuộc N thì đều lớn hơn 1 ( loại )
+) Với a>2 ; \(n\in N\) => Tất cả đều lớn hơn 1 ( loại )
Vậy với a=1 ; \(n\in N\) thì \(a^n=1\)

\(A=\dfrac{n-2}{n-5}=\dfrac{n-5+3}{n-5}=1+\dfrac{3}{n-5}\)
n-5 là ước nguyên của 3
n-5=1=> n = 6
n-5=3=> n =8
n-5 = -1=> n =4
n-5 = -3 => n=2
mink chỉ biết phần a thôi bạn ạ
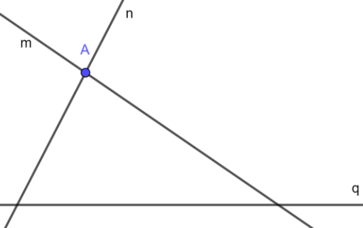
Đáp án là C
Dựa vào hình vẽ ta thấy, điểm A thuộc đường thẳng m và n, điểm A không thuộc đường thẳng q